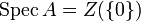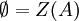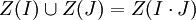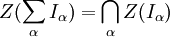Faisceau structural

En mathématique, le spectre d'un anneau commutatif unitaire A désigne l'ensemble des idéaux premiers de A. Cet ensemble est muni d'une topologie (de Zariski) et d'un faisceau d'anneaux commutatifs unitaires qui en font un espace topologique annelé en anneaux locaux. Cet espace est alors appelé un schéma affine et il sert d'espace de base pour la construction des schémas en géométrie algébrique.

Sommaire 1 Définition ensembliste 2 Topologie de Zariski 2.1 Définition 3 Propriétés topologiques 3.1 Points particuliers 3.2 Séparation et compacité 3.3 Applications continues 4 Faisceau structural

Définition ensembliste

Le spectre d'un anneau commutatif unitaire A est l'ensemble de ses idéaux premiers. On le note .

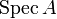• Spec ℤ correspond l'ensemble des nombres premiers et 0. Les nombres premiers p correspondent aux idéaux premiers pℤ, et 0 correspond à l'idéal nul.

• Spec ℝ[X] contient 0 (idéal nul); ℝ (chaque réel r correspond à l'idéal premier (X-r)ℝ[X]), et les couples de nombres complexes conjugués (z, z') correspondant à l'idéal premier (X-z)(X-z')ℝ[X].

Topologie de Zariski

Définition

À tout idéal I de A, on associe Z(I), qui est l'ensemble des idéaux premiers de A qui contiennent I.

Remarquons que :

• 
• 
• 
• 

Les Z(I) forment donc les fermés d'une topologie sur 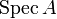, que l'on appelle topologie de Zariski.

Pour tout élément f de A, l'ensemble des idéaux premiers de A ne contenant pas f est un ouvert de Zariski dans 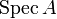(c'est le complémentaire de Z(fA)) noté D(f) ; on appelle parfois ouverts distingués ou ouverts principaux les ouverts de cette forme, ils constituent une base de la topologie de Zariski sur .

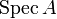Propriétés topologiques

Points particuliers

Un point de 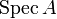est fermé si le singleton correspondant est une partie fermée de 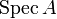. Le point défini par un idéal premier est fermé si et seulement si l'idéal est maximal. Si A est non nul, alors Spec A a toujours des points fermés. Mais contrairement à ce qui se passe pour les topologies métriques, tous les points ne sont pas fermés en général. Dans les exemples Spec ℤ et Spec ℝ[X], il existe un idéal premier (l'idéal nul) non maximal.

Puisqu'un point x de Spec A n'est pas nécessairement fermé, on peut considérer son adhérence (enfin celle du singleton { x }) dans Spec A pour la topologie de Zariski. On dit qu'un point est générique s'il n'appartient à l'adhérence d'aucun autre point. Il est facile de voir qu'un point correspondant à un idéal premier est générique si et seulement si l'idéal premier est minimal (c'est-à-dire ne contenant aucun autre idéal premier). Ainsi, si A est intègre, l'idéal nul est un idéal premier, évidemment minimal, et correspond donc à un point générique de Spec A. C'est aussi l'unique point générique de Spec A. L'adhérence du point générique est l'espace tout entier (c'est un point dense) !

Si A n'est pas intègre, il peut y avoir plusieurs points génériques. L'adhérence de chacun de ces points génériques est un fermé de Spec A appelée une composante irréductible de Spec A.

Exemple Si A=ℝ[X, Y]/(XY) (quotient par l'idéal engendré par le polynôme XY). Alors Spec A possède deux points génériques correspondant aux idéaux engendré par X et par Y. Les composantes irréductibles correspondantes sont homéomorphes à Spec ℝ[Z].

Séparation et compacité

L'espace Spec A est quasi-compact: de tout recouvrement ouvert {U_i}_i de Spec A, on peut en extraire un sous-recouvrement fini. En effet, U_i est le complémentaire de Z(I_i) et Z(∑_i I_i), qui est l'intersection des Z(I_i), est vide. Donc ∑_i I_i=A. Cela implique que l'unité 1 de A appartient à la somme d'un nombre fini d'idéaux I_i. Les ouverts U_i correspondant aux complémentaires de ces Z(I_i) recouvrent Spec A.

Par contre, comme nous l'avons vu plus haut, un point n'est pas nécessairement fermé. Donc Spec A n'a aucune chance d'être un espace séparé en général. Néanmoins Spec A possède la propriété T₀. De plus, si on interprète la separation d'un espace topologique X par le fait que la diagonale de X × X (produit cartésien muni de la topologie produit) est fermée, alors Spec A devient séparé dans le monde des schémas à condition de définir convenablemnt le produit (produit fibré) de Spec A par lui-meme.

Applications continues

Soit h : A -> B un homomorphisme d'anneaux. Pour tout idéal premier P de B, h^-1(P) est un idéal premier de A, ce qui définit une application Spec h : Spec B -> Spec A. De plus, pour tout idéal J de B, h^-1(Z(J))=Z(h^-1(J)) est fermé. Donc Spec h est une application continue.

Exemples

• Si h est la surjection canonique A -> A/I correspondant au quotient de A par un idéal I, alors Spec h est une immersion fermée et identifie Spec A/I à Z(I) muni de la topologie induite par celle de Spec A.
• Soit f un élément non-nilpotent de A, soit h : A -> A_f l'homomorphisme de localisation a -> a/1. Alors Spec h est une immersion ouverte et identifie Spec A_f à l'ouvert principal D(f).
• Pour tout anneau A, il existe un unique homomorphisme d'anneaux ℤ -> A. Ce qui donne une application continue Spec A -> Spec ℤ. Si A est de caractéristique p positive avec p premier, alors l'image de cette application est le point pℤ.

Faisceau structural

À isomorphisme près, il existe un unique faisceau d'anneaux commutatifs sur l'espace topologique 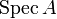dont l'anneau des sections sur un ouvert de la forme D(f) (pour 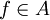) s'identifie à l'anneau localisé A_f.

La donnée de l'espace topologique 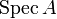muni de ce faisceau d'anneaux (appelé faisceau structural) constitue un espace topologique annelé. Si U est un ouvert de 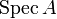, l'anneau des sections sur U du faisceau structural est appelé par abus de langage anneau des fonctions régulières sur U.

Pour tout idéal premier 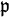de A, l'anneau des germes de fonctions régulières en 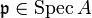s'identifie au localisé 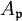de A en l'idéal premier 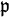. L'espace annelé 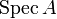est ainsi un espace topologique annelé en anneaux locaux ; par définition, il s'agit d'un schéma affine.

• Portail des mathématiques