Faisceau De Droites

Faisceau De Droites

Faisceau de droites

En géométrie projective, un faisceau de droites est un ensemble de droites passant par un point.

En géométrie affine, on distinguera un ensemble de droites parallèles (le point commun est à l'infini) et un ensemble de droites passant par un point.

On peut également définir dans un espace affine de direction 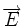\overrightarrow E, un faisceau d'hyperplan comme une famille d'hyperplans, de rang deux.

Ainsi il existe deux hyperplans H1 et H2 d'équation f1(M) = 0 et f2(M) = 0 tels que tout hyperplan du faisceau ait une équation de la forme (λf1 + μf2)(M) = 0. On parle alors d'un faisceau de base H1 et H2.

Cas parallèle

Si H1 et H2 ont la même direction (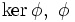\ker\phi,\,\, \phi étant une forme linéaire sur 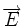\overrightarrow E), il en sera de même de H.

Réciproquement, tout hyperplan de direction kerφ admet une équation de la forme (λf1 + μf2)(M) = 0.

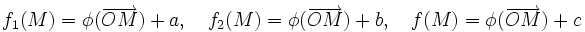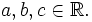En effet, on aura par exemple f_1(M)= \phi(\overrightarrow{OM})+a,\quad f_2(M)=\phi(\overrightarrow{OM})+b,\quad f(M)=\phi(\overrightarrow{OM})+c où a,b,c\in\Bbb R. Mais il existe toujours 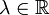\lambda\in\Bbb R tel que c = λa + (1 − λ)b d'où il résulte f = λf1 + (1 − λ)f2.

Cas sécant

Si les parties linéaires de f1 et f2 ne sont pas proportionnelles, 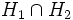H_1\cap H_2 est de dimension n-2. Tout hyperplan contenant 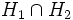H_1\cap H_2 appartient alors au faisceau de base H1,H2.

Soit en effet kerφ1, kerφ2, kerφ les directions respectives de H1,H2,H. Comme 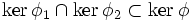\ker\phi_1\cap\ker\phi_2\subset \ker\phi, on a φ = λφ1 + μφ2.

(On peut prouver ce résultat d'algèbre linéaire en considérant l'application qui à 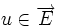u\in\overrightarrow E associe le triplet 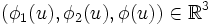(\phi_1(u),\phi_2(u),\phi(u))\in\Bbb R^3; son noyau est de dimension n-2 donc elle est de rang 2 d'après le théorème du rang. Ainsi φ1,φ2,φ sont liés et comme φ1,φ2 sont indépendants le résultat en découle.)

Cas particuliers

C'est bien entendu le cas des droites parallèles dans le plan, celui des droites passant par un point (défini comme intersection de deux droites qui fournissent alors une base de ce faisceau).

C'est encore le cas des plan parallèles de l'espace ou des plans contenant une droite donnée (définie comme intersection de deux plans qui fournissent une base du faisceau)

application élémentaire

Soit les droites d'équation 2x + 3y − 1 = 0 et x + 2y + 2 = 0; soit 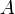A\, leur point d'intersection. Trouver l'équation de la droite passant par A et le point (1, − 2)

La droite cherchée appartient au faisceau des droites passant par A.

Son équation est de la forme λ(2x + 3y − 1) + μ(x + 2y + 2) = 0. Elle passe par (1, − 2) si et seulement si − 5λ − μ = 0. On peut prendre λ = 1 et μ = − 5 d'où l'équation cherchée

3x + 7y + 11 = 0.

orthocentre de trois tangentes à une parabole


  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Faisceau de droites ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Faisceau De Droites de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • Faisceau de droites — En géométrie projective, un faisceau de droites est un ensemble de droites passant par un point. En géométrie affine, on distinguera un ensemble de droites parallèles (le point commun est à l infini) et un ensemble de droites passant par un point …   Wikipédia en Français

  • faisceau — [ fɛso ] n. m. • 1549; faissel, fasselXIIe; lat. pop. ° fascellus, de fascis 1 ♦ Assemblage de choses semblables, de forme allongée, liées ensemble. Balai fait d un faisceau de brindilles. Faisceau de branchages (⇒ fagot) , de végétaux (⇒ 1.… …   Encyclopédie Universelle

  • Faisceau Harmonique — Étant donné quatre droites concourantes ou parallèles, on peut montrer que le birapport des quatre points que l on obtient par intersection avec une sécante à ces 4 droites ne dépend pas de la sécante. De plus il est égal au rapport des mesures… …   Wikipédia en Français

  • Faisceau d'hyperplans — Faisceau de droites En géométrie projective, un faisceau de droites est un ensemble de droites passant par un point. En géométrie affine, on distinguera un ensemble de droites parallèles (le point commun est à l infini) et un ensemble de droites… …   Wikipédia en Français

  • Faisceau harmonique — En géométrie, étant donné quatre droites concourantes ou parallèles, on peut montrer que le birapport des quatre points que l on obtient par intersection avec une sécante à ces 4 droites ne dépend pas de la sécante ; de plus il est égal au… …   Wikipédia en Français

  • Faisceau — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Faisceau », sur le Wiktionnaire (dictionnaire universel) En tant qu objet, un faisceau est un ensemble …   Wikipédia en Français

  • Propriétés métriques des droites et plans — En géométrie euclidienne, c est à dire dans le plan et l espace muni d une distance et d un produit scalaire, les droites et les plans possèdent des propriétés métriques permettant de les caractériser grâce à un point et un vecteur, dit normal.… …   Wikipédia en Français

  • Construction D'un Cercle Point Par Point — Sommaire 1 Premier exemple 1.1 Méthode des chemins de fer 1.2 Explication de cette méthode 1.3 Fonction homographique mise en jeu …   Wikipédia en Français

  • Construction d'un cercle point par point — Sommaire 1 Premier exemple 1.1 Méthode des chemins de fer 1.2 Explication de cette méthode 1.3 Fonction homographique mise en jeu …   Wikipédia en Français

  • Quadrilatere complet — Quadrilatère complet Un quadrilatère complet est une figure de géométrie plane constituée de quatre droites dont deux quelconques ne sont pas parallèles ni trois quelconques concourantes. Une autre manière de définir un quadrilatère complet est… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”