Faisceau harmonique

Faisceau harmonique

En géométrie, étant donné quatre droites concourantes ou parallèles, on peut montrer que le birapport des quatre points que l'on obtient par intersection avec une sécante à ces 4 droites ne dépend pas de la sécante ; de plus il est égal au rapport des mesures algébriques des 3 points d'intersections (dans l'ordre adéquat) pour une sécante à trois seulement de ces quatre droites et parallèle à la quatrième. Ce birapport de 4 points est appelé également « birapport des quatre droites ». Quand ce birapport égale -1 on dit que les quatre droites (concourantes ou parallèles) forment un faisceau harmonique. Bien qu'exprimé ici en géométrie affine, il s'agit fondamentalement d'une notion de géométrie projective. Les deux cas (droites concourantes et droites parallèles) sont réunis en un seul. Le cas où la sécante est parallèle à l'une des quatre droites n'existe pas (ou plutôt il est intégré au cas général). Le birapport de quatre droites concourantes est la notion duale du birapport de quatre points alignés. La notion de faisceau harmonique est la notion duale de celle de division harmonique.

Démonstration analytique

Les quatre droites sont données par des équations fi(M) = 0, (i = 1,2,3,4) où fi est une forme affine de partie linéaire ϕi. Supposons la droite \mathcal D définie par un point A\, et un vecteur directeur u\,.

Un point de \mathcal D est sur la droite \mathcal D_i si, et seulement si, M = A + λiu avec fi(A) + λiϕi(u) = 0 soit \lambda_i=-\frac{f_i(A)}{\phi_i(u)}.

La condition de division harmonique s'écrit alors

\frac{\lambda_2-\lambda_1}{\lambda_4-\lambda_1}=-\frac{\lambda_2-\lambda_3}{\lambda_4-\lambda_3}

ou encore après avoir remplacé les λi par leur valeur et réduit les fractions au même dénominateur

\frac{f_1(A)\phi_2(u)-f_2(A)\phi_1(u)}{f_1(A)\phi_4(u)-f_4(A)\phi_1(u)}=- \frac{f_3(A)\phi_2(u)-f_2(A)\phi_3(u)}{ f_3(A)\phi_4(u)-f_4(A)\phi_3(u)}

On peut également mettre cette expression sous la forme :

(1)\qquad\begin{vmatrix}f_1(A)&f_2(A)\\\phi_1(u)&\phi_2(u)\end{vmatrix} \begin{vmatrix}f_3(A)&f_4(A)\\\phi_3(u)&\phi_4(u)\end{vmatrix} =-\begin{vmatrix}f_3(A)&f_2(A)\\\phi_3(u)&\phi_2(u)\end{vmatrix} \begin{vmatrix}f_1(A)&f_4(A)\\\phi_1(u)&\phi_4(u)\end{vmatrix}.

Les droites D1,D3 engendrant le faisceau de droites auquel appartiennent D2 et D4, il existe des constantes α,β telles que f2 = f1 + αf3 et f4 = f1 + βf3.

Notons que ce résultat est encore vrai dans le cas des droites parallèles.

En remplaçant ces expressions dans l'égalité (1), les déterminants se simplifient immédiatement (par combinaison de colonnes) ce qui conduit à l'égalité

\alpha\begin{vmatrix}f_1(A)&f_3(A)\\\phi_1(u)&\phi_3(u)\end{vmatrix}^2=-\beta \begin{vmatrix}f_1(a)&f_3(A)\\\phi_1(u)&\phi_3(u)\end{vmatrix}^2

La condition d'harmonie équivaut donc à α = − β.

La condition ne dépend donc que des quatre droites du faisceau et non de \mathcal D dont les éléments caractéristiques ont disparu.

Invariance du birapport

Si l'on suppose que le birapport des quatre points vaut K, il suffit de remplacer dans la preuve si-dessus, le signe "-" par K. La condition finale devenant α = Kβ.

Là encore ce birapport ne dépend pas de la droite sécante.

Démonstration géométrique

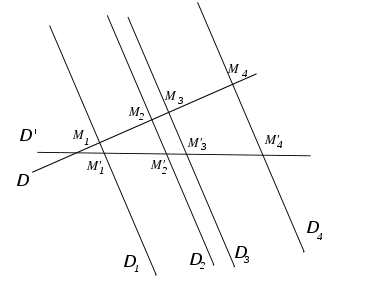
-- Cas des droites parallèles FaisceauParall.svg

Soit \mathcal D,\mathcal D' deux sécantes. Le théorème de Thalès permet d'affirmer que tous les quotients \frac{\overline{M_iM_j}}{ \overline{M'_iM'_j} } sont égaux.

Il en résulte immédiatement que \frac{\overline{M'_1M'_2}}{\overline{M'_1M'_4} }\frac{\overline{M'_3M'_4}}{\overline{M'_3M'_2}}= \frac{\overline{M_1M_2}}{\overline{M_1M_4} }\frac{\overline{M_3M_4}}{\overline{M_3M_2}}=-1.

Les points M'i sont donc en division harmonique.

Remarque : Plus généralement, le birapport est donc conservé.

-- Cas des droites issues d'un point

Birraport Faisceau.svg

Quite à translater la droite \mathcal D', ce qui ne change pas le birapport des quatre points, on peut supposer que \mathcal D'\cap\mathcal D_1=\mathcal D\cap\mathcal D_1=M_1.

On mène ensuite les parallèles à \mathcal D_1 issues de M3 et M'3 qui coupent \mathcal D_2 en N2 et N'2 et \mathcal D_4 en N4 et N'4.

Le théorème de Thalès affirme

\frac{\overline{M_2M_1}}{\overline{M_2M_3}}=\frac{\overline{OM_1}}{\overline{N_2M_3}} et \frac{\overline{M_4M_1}}{\overline{M_4M_3} }=\frac{\overline{OM_1}}{ \overline{N_4M_3}};

les points M1,M2,M3,M4 étant en division harmonique, on a \overline{M_4M_1}/\overline{M_4M_3}=-\overline{M_2M_1}/\overline{M_2M_3} ce qui conduit à \overline{N_4M_3}=-\overline{N_2M_3} de sorte que M3 est le milieu de [N2,N4].

Par application du même théorème de Thales aux droites \mathcal D_2,\mathcal D_3,\mathcal D_4 on déduit que M'3 est le milieu de [N'2,N'4].

De là \frac{\overline{M'_2M'_1}}{\overline{M'_2M'_3}}=\frac{\overline{OM_1}}{\overline{N'_2M'_3}}=- \frac{\overline{OM_1}}{ \overline{N'_4M'_3}}=-\frac{\overline{M'_4M'_1}}{\overline{M'_4M'_3} },

Remarque 1: on a prouvé au passage que si un faisceau est harmonique, toute parallèle à une des droites issue de l'un des points d'une séquante est au milieu des points d'intersection de cette parallèle et des deux autres droites.

Remarque 2 (conservation du birapport): Rien n'est modifié substantiellement si le birapport des quatre points vaut K à la place de -1. Il suffit d'introduire la constance K à la place du changement de signe.


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Faisceau harmonique de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Faisceau Harmonique — Étant donné quatre droites concourantes ou parallèles, on peut montrer que le birapport des quatre points que l on obtient par intersection avec une sécante à ces 4 droites ne dépend pas de la sécante. De plus il est égal au rapport des mesures… …   Wikipédia en Français

  • Pinceau ou faisceau harmonique — ● Pinceau ou faisceau harmonique pinceau ordonné dont le birapport vaut (−1) …   Encyclopédie Universelle

  • harmonique — [ armɔnik ] adj. et n. m. ou f. • XIVe; lat. harmonicus, gr. harmonikos 1 ♦ Qui concourt à l harmonie musicale. ♢ Se dit de certains sons, de certains rapports ou assemblages de sons caractéristiques, en harmonie. Gamme, échelle harmonique. ⇒… …   Encyclopédie Universelle

  • faisceau — [ fɛso ] n. m. • 1549; faissel, fasselXIIe; lat. pop. ° fascellus, de fascis 1 ♦ Assemblage de choses semblables, de forme allongée, liées ensemble. Balai fait d un faisceau de brindilles. Faisceau de branchages (⇒ fagot) , de végétaux (⇒ 1.… …   Encyclopédie Universelle

  • harmonique — (ar mo ni k ) adj. 1°   Dont toutes les parties concourent à un même but ou effet. •   Le temps est venu qu il faut remettre les anciens ordres et cette relation harmonique qui doit exister entre un commandement légitime et une obéissance… …   Dictionnaire de la Langue Française d'Émile Littré

  • Division Harmonique — (A, B, C, D) est une division harmonique : En géométrie affine quatre points alignés sont en division harmonique quand ils vérifient l égalité des rappo …   Wikipédia en Français

  • Division harmonique — (A, B, C, D) est une division harmonique : En géométrie affine quatre points alignés sont en division harmonique quand ils vérifient l égalité des rapports de mesure algébrique indiquée ci contre. El …   Wikipédia en Français

  • Generation de seconde harmonique — Génération de seconde harmonique La génération de seconde harmonique (GSH; également appelé doublage de fréquence) est un processus d optique non linéaire dans lequel des photons interagissant avec un matériau non linéaire sont combinés pour… …   Wikipédia en Français

  • Génération De Seconde Harmonique — La génération de seconde harmonique (GSH; également appelé doublage de fréquence) est un processus d optique non linéaire dans lequel des photons interagissant avec un matériau non linéaire sont combinés pour former de nouveaux photons avec le… …   Wikipédia en Français

  • Génération de second harmonique — Génération de seconde harmonique La génération de seconde harmonique (GSH; également appelé doublage de fréquence) est un processus d optique non linéaire dans lequel des photons interagissant avec un matériau non linéaire sont combinés pour… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”