Facteur de puissance

Le facteur de puissance est une caractéristique d'un récepteur électrique.

Pour un dipôle électrique alimenté en régime de courant variable au cours du temps (sinusoïdal ou non), il est égal à la puissance active consommée par ce dipôle divisée par le produit des valeurs efficaces du courant et de la tension (puissance apparente). Il est toujours compris entre 1 et 0.

$\lambda = \frac{P}{UI} = \frac PS$

En particulier, si le courant et la tension sont des fonctions sinusoïdales du temps, le facteur de puissance est égal au cosinus du déphasage entre le courant et la tension.

λ = cos φ

Le facteur de puissance est un paramètre qui rend compte de l'efficacité qu'a un dipôle pour consommer de la puissance lorsqu'il est traversé par un courant. Une comparaison mécanique possible serait le facteur d'embrayage d'une boîte de vitesses :

lorsque la pédale d'embrayage est enfoncée, le moteur tourne (le courant circule) mais ne transmet aucune puissance au véhicule ; le facteur de puissance est nul
lorsque la pédale d'embrayage est relevée, le moteur tourne et toute sa quantité de mouvement est transmise au véhicule pour produire de la puissance motrice ; le facteur de puissance est unitaire
lorsque l'on fait patiner l'embrayage, on est dans une situation intermédiaire, cela correspond au cas où le facteur de puissance est compris entre 0 et 1

Sommaire

1 Importance du facteur de puissance pour le distributeur
2 Facteur de puissance en régime sinusoïdal de courant
3 Facteur de puissance en régime non-sinusoïdal de courant
- 3.1 Définitions
4 Voir aussi
- 4.1 Liens internes
- 4.2 Liens externes
5 Notes

Importance du facteur de puissance pour le distributeur

Les distributeurs d'électricité facturent généralement la puissance active consommée sur la base de la mesure réalisée au point de fourniture, alors que les pertes dans les lignes sont facturées globalement. Or celles-ci dépendent de l'intensité apparente appelée par les consommateurs (pertes par effet Joule). Si le facteur de puissance d'une installation est faible, l'intensité appelée est grande mais la puissance consommée est faible. C'est pourquoi, pour les gros consommateurs (installations raccordées à la haute tension), la facturation ne tient pas uniquement compte de la puissance active consommée. En France, cette facturation est très complexe. Elle est réglementée par le ministère de l'industrie : JO n° 170 du 23 juillet 2002, pages 12600 et suivantes. Elle ne concerne actuellement que les clients raccordés à la haute tension, les mois d'hiver et au cours des heures pleines.

Exemple : Soit un dipôle purement réactif (un condensateur par exemple) traversé par un courant d'intensité 1 A sous 220 volts. Ce dipôle introduisant un déphasage de $π / 2$ entre la tension et le courant, le facteur de puissance $cos(π / 2)$ est nul. La puissance active, facturée par le distributeur, est donc nulle. Pourtant, la puissance apparente vaut 220 VA et il passe réellement 1A dans la ligne, ce qui implique des pertes par effet joule et oblige le distributeur à dimensionner son matériel (transformateurs, lignes,...) en conséquence.

Pour le consommateur, la puissance réactive ainsi "consommée" n'est en fait qu'un échange de charges électriques entre le générateur et le dipôle, de puissance moyenne nulle sur la période.

Facteur de puissance en régime sinusoïdal de courant

Effets du facteur de puissance

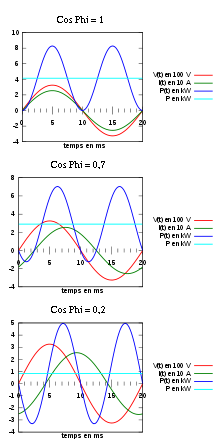
Courbes représentant l'évolution dans le temps de la tension V(t), du courant I(t) et de la puissance P(t) en fonction du temps ainsi que la valeur moyenne de la puissance. Courbe du haut : facteur de puissance = 1 ; courbe du milieu : 0,7 ; courbe du bas : 0,2.

Le schéma ci-contre représente la puissance instantanée (produit de la tension et du courant instantanés) consommée par un dipôle soumis à une tension de 230 V et traversé par un courant de 18 A dans 3 cas :

le facteur de puissance est égal à 1 (valeur maximale) : la tension et le courant sont en phase (ils sont nuls aux mêmes instants), la puissance instantanée est toujours positive et la puissance moyenne est maximale
le facteur de puissance est égal à 0,7 (valeur intermédiaire) : le courant suit toujours une courbe périodique, mais elle est « en retard » comparativement à la courbe de la tension. La puissance prend par moment des valeurs négatives, le dipôle refoule périodiquement de l’énergie sur le réseau.
le facteur de puissance est égal à 0,2 (valeur faible) : le courant est le même, la puissance instantanée fluctue avec la même amplitude, mais elle est fortement décalée vers le bas par rapport aux courbes précédentes. La puissance moyenne est faible : 20 % de la puissance mise en jeu lorsque le facteur de puissance est unitaire.

La figure visualise la situation d'un dipôle inductif tel une bobine : le courant est en retard sur la tension. La puissance périodiquement restituée provient de l'énergie magnétique stockée.

Une situation "symétrique" se produit avec un dipôle capacitif : dans ce cas, le courant est en avance sur la tension. La puissance périodiquement restituée provient de l'énergie de la charge électrique stockée.

Les effets de dipôles plus complexes (par exemple un grand nombre de télévisions) peuvent modifier la tension nominale du réseau d'alimentation, engendrer des perturbations de l'onde sinusoïdale et produire des courants harmoniques susceptibles de perturber le bon fonctionnements d'autres appareils. Le gestionnaire du réseau de distribution s'engage à maintenir un taux de distorsion harmonique acceptable, quitte à imposer des contraintes à certains clients qui les génèrent.

Les facteurs de puissance dégradés d’un grand nombre de points de consommation sont compensés de diverses manières :

Au niveau de la production où certains alternateurs des usines de production sont appelés à fonctionner en compensation synchrone, ce qui réduit d’autant la puissance active que l’usine est capable de produire. Cette méthode ne permet toutefois pas de corriger toutes les distorsions harmoniques.
Au niveau du réseau où ont été installés des compensateurs statiques d'énergie réactive ou plus généralement des systèmes de transmission flexible en courant alternatif (FACTS).

Situation d’une inductance (self)^{[réf. nécessaire]}

Considérons une bobine et l’équation différentielle du modèle (courant monophasé) comprenant une self d’inductance $L$ branchée en série avec une résistance de valeur $r$ :

$u(t) = L \frac{\mathrm di(t)}{\mathrm dt} + r i(t)$

Pour une fréquence $f$ avec sa pulsation $ω = 2π f$ , on suppose que le courant est sinusoïdal $i (t) = I sin(ω t)$ d’intensité nominale $I$ . L’équation différentielle conduit à

u (t) = I L ωcos(ω t) + I r sin(ω t)

En définissant $U$ et $\varphi$ par les relations

U sin φ = I L ω

U cos φ = I r

on en tire

$\tan \varphi = \frac{L \omega}{ r }$ et

$U = I r \sqrt{1+ \tan^2 \varphi} = \frac{I r }{\cos \varphi}$ ,

soit $u (t) = U sin(ω t + φ)$ et la puissance instantanée $p (t) = u (t) i (t)$ .

Cette solution périodique du modèle de la self montre que le courant est en retard sur la tension avec un déphasage $\varphi$ . La situation décrite dans la figure ci-dessus correspond au cas d’une inductance.

La puissance moyenne (active) atteint

$P_\text{moy} = \frac{1}{2} r I^2 = \frac{1}{2} U I \cos \varphi$ .

Supposons d’autre part de ce système soit alimenté par un réseau dont la résistance est $R$ . Les pertes de transport (dues à l’effet Joule) $P p e r t e s (t) = R i 2 (t)$ dont la moyenne est $P pertes moy = R I 2 / 2$ Ainsi les pertes moyennes relativement à la puissance fournie atteignent

$P_\text{pertes relat} = \frac{R I}{U \cos \varphi}$ .

Les pertes relatives augmentent donc en proportion inverse du facteur de puissance.

Situation d’une capacité (condensateur)^{[réf. nécessaire]}

Considérons un dipôle capacitif comprenant un condensateur de capacité $C$ branché en parallèle avec une résistance de valeur $r$ . L’équation différentielle de ce système (courant monophasé) s’écrit :

$i(t) = C \frac{\mathrm du(t)}{\mathrm dt} + \frac{u(t)}{r}$

Pour une fréquence $f$ avec sa pulsation $ω = 2π f$ , on suppose que la tension est sinusoïdale $u (t) = U sin(ω t)$ de tension nominale $U$ . L’équation différentielle conduit à

$i(t) = U C \omega \cos(\omega t) + \frac{U}{r} \sin(\omega t)$

En définissant $I$ et $\varphi$ par les relations

I sin φ = U C ω

et $I \cos \varphi = \frac{U}{r}$ ,

on en tire

tan φ = C ω r

$r I = U \sqrt{1+ \tan^2 \varphi} = U \cos \varphi$ ,

soit $U (t) = I sin(ω t + φ)$ et la puissance instantanée $p (t) = u (t) i (t)$ .

La solution périodique de ce modèle capacitif montre que le courant est en avance sur la tension avec un déphasage $\varphi$ .

La puissance moyenne (active) atteint

$P_\text{moy} = \frac{1}{2} \frac{U^2}{r} = \frac{1}{2} U I \cos \varphi$ .

Supposons d’autre part de ce système soit alimenté par un réseau dont la résistance est $R$ . Les pertes de transport (dues à l’effet Joule) $P pertes (t) = R i 2 (t)$ dont la moyenne est $P pertes moy = R I 2 / 2$ Ainsi les pertes moyennes relativement à la puissance fournie atteignent

$P_\text{pertes relat} = \frac{R I}{U \cos \varphi}$ .

Les pertes relatives augmentent donc en proportion inverse du facteur de puissance.

Une analogie mécanique illustrant le facteur de puissance et ses effets

Considérons un système mécanique constitué de deux poulies (fixées sur deux axes) reliées entre-elles par un câble (tel un téléski simplifié). La poulie A étant mise en mouvement par une force extérieure (un moteur), l’autre est entraînée par le câble dans un mouvement semblable. Supposons que le mouvement transmis à A soit sinusoïdal et que les masses des composants soient négligeables.

Les analogies avec des dipôles sont les suivantes :

La poulie A s’apparente à la production, la poulie B à la consommation.
Le câble s’apparente au réseau électrique de transport.
La vitesse du câble correspond à la tension, la force de traction à l’intensité.
Le produit de la force par la vitesse correspond à la puissance mécanique transmise.
Un frein s’exerçant sur une poulie correspond à une consommation de puissance.
Un volant d'inertie ajouté à une poulie reflète une capacité.
Un ressort spiral fixé à une poulie reflète une inductance.

On peut concevoir les effets suivants qui se manifestent également dans le monde électrique :

Sans masse (ni frein, ni volant, ni ressort), il n’y a pas de puissance transmise.
Un frein sur la poulie B implique un facteur de puissance $cos φ = 1$ .
Un ressort ajouté à la poulie B implique un effort supplémentaire du câble pour tendre le ressort, puis pour récupérer l’énergie potentielle restituée lorsque le câble change de sens ( $cos φ < 1$ ). Le moteur devra périodiquement fournir et absorber cette puissance transportée par le câble.
Le moteur est soulagé des efforts précédents lorsqu’un volant d'inertie est ajouté à la poulie A. Le câble transfère successivement et réciproquement l’énergie potentielle du ressort à l’énergie cinétique du volant. L’énergie totale est constante lorsque les caractéristiques des deux éléments sont appropriées.
C’est encore mieux si le volant et fixé directement sur la poulie B : on évite des pertes lorsque l’énergie réactive est produite près du lieu de sa consommation.
Si elles ne sont pas négligées, la masse et l’élasticité du câble correspondent respectivement aux caractères de capacité et d’inductance de la ligne électrique.
Si le câble est élastique (mais de masse faible), l’ampleur du mouvement de la poulie B est significativement plus important que celui de la poulie A sous certaines conditions : l’analogie est une élévation de la tension au niveau de la distribution.
En plaçant le ressort en A et le volant en B, la masse peine à se mettre en mouvement par l’élasticité du câble : l’analogie est une baisse de tension au niveau de la distribution.

Amélioration du facteur de puissance

En triphasé, on utilise les définitions des puissances suivantes pour intermédiaires de calculs :

La puissance apparente : $S = U \cdot I \cdot \sqrt3$ ,
La puissance réactive : $Q = U \cdot I \cdot \sqrt3 \cdot \sin \varphi$ ,
La puissance active : $P = U \cdot I \cdot \sqrt3 \cdot \cos \varphi$ , d'où $Q = \tan \varphi \cdot P$

En France, pour les industriels alimentés en haute tension, la partie de puissance réactive totale $Q T$ est gratuite à concurrence de $0,4 P T$ . L'excédent est facturé pendant les heures pleines des mois d'hiver (Décret n° 2002-1014 du 19 juillet 2002^[1]). Il est toujours judicieux de modifier l'impédance de sa charge afin de minimiser sa puissance réactive.

Utilisation de batterie de condensateurs

A l'aide de la méthode de Boucherot, on détermine la valeur minimale de $Q C$ , puissance réactive toujours négative des condensateurs, de manière à ce que

$Q_T + Q_C = 0,4 \cdot P_T$ (L'industrie utilisant majoritairement des machines inductives, $Q T$ est positive)

On en déduit ensuite la valeur minimale des capacités à ajouter au circuit pour respecter le cahier des charges prévu.

Ces batteries de condensateurs sont parfois agencées en filtre anti-harmonique.

Utilisation de compensateurs synchrones

Certaines entreprises utilisent des génératrices synchrones pour produire des courants en avance sur la tension afin de compenser le retard des courants consommés par les moteurs électriques.

Utilisation de FACTS

Les systèmes FACTS sont des équipements à base d'électronique de puissance qui ont pour vocation d'améliorer la qualité de l'énergie électrique. Parmi eux, certains comme les SVC permettent à la fois une régulation de la tension et une amélioration du facteur de puissance.

Facteur de puissance et facteur de qualité

En électronique on définit un facteur de qualité pour les dipôles oscillants qui est d'autant plus grand que le facteur de puissance est faible. La raison en est que la perspective n'est pas la même en électronique et en électrotechnique.

Pour l'électrotechnicien le but ultime est d'utiliser l'énergie électrique en la convertissant soit en chaleur, soit en lumière, soit en énergie mécanique.
En électronique, lorsque l'on cherche à obtenir des oscillations, la transformation d'énergie en chaleur est perçue comme une perte et non comme une efficacité.

Facteur de puissance en régime non-sinusoïdal de courant

Dans le cas où le courant absorbé n'est pas sinusoïdal, le problème est plus complexe : même si le courant est en phase avec la tension (le facteur de déplacement est nul), la puissance n'est pas égale au produit des valeurs efficaces

Deux méthodes d'études sont généralement utilisées :

Le théorème de Boucherot généralisé
Le taux d'harmonique

Définitions

Le calcul de la puissance active donne comme résultat :

$P = U \cdot I_1 \cdot \cos \varphi_1$

D'autre part la puissance apparente $S$ peut s'écrire :

$S =\sqrt { P^2 + Q^2 +D^2}$

Avec les définitions des intermédiaires de calcul suivants :

La puissance réactive : $Q = U \cdot I_1 \cdot \sin \varphi_1$
La puissance déformante : $D$ telle que $D^2 = U^2 (I_2^2 + I_3^2 + ... + I_n^2 ) = U^2 \cdot I_h^2$

et :

$I 1$ : la valeur efficace du fondamental du courant
$I h$ : la valeur efficace de l'ensemble des harmoniques de rang supérieur à 1 du courant
$\varphi_1$ : la valeur du déphasage de l'harmonique $i 1 (t)$ par rapport à la tension.
$cos φ 1$ : facteur de déplacement

Détail des calculs on a : $S^2 =U^2 \cdot I^2$

avec :

$U^2 =U_1^2$

$I^2 =I_1^2 +I_2^2 + ... I_n^2 + ...$

d'où :

$S^2 = U^2 \cdot I_1^2 + U^2 \cdot I_2^2+ ... + U^2 \cdot I_n^2+ ...$

$S^2 = (U\cdot I_1 \cos \varphi_1)^2 + (U\cdot I_1 \sin \varphi_1)^2 + U^2 \cdot I_2^2+ ... + U^2 \cdot I_n^2+ ...$

$S^2 = P^2 + Q^2 + U^2 \cdot ( I_2^2+ ... + I_n^2+ ...)$

$S^2 = P^2 + Q^2 + U^2 \cdot I_h^2$

Voir aussi

Correcteur du facteur de puissance

Liens internes

Liens externes

(fr) http://www.intersections.schneider-electric.fr/stock_images/telec/1/n3/GT_Perturbations.pdf - page 3
(fr) http://www.intersections.schneider-electric.fr/stock_images/telec/1/n3/GT16_CER.pdf - article concernant la compensation de l'énergie réactive.

Notes

↑ Décret n° 2002-1014 du 19 juillet 2002 fixant les tarifs d'utilisation des réseaux publics de transport et de distribution d'électricité en application de l'article 4 de la loi n° 2000-108 du 10 février 2000 relative à la modernisation et au développement du service public de l'électricité

Portail de l’électricité et de l’électronique

Catégories :

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Facteur de puissance de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Facteur De Puissance — Le facteur de puissance est une caractéristique d un récepteur électrique. Pour un dipôle électrique alimenté en régime de courant variable au cours du temps (sinusoïdal ou non), il est égal à la puissance active consommée par ce dipôle divisée… … Wikipédia en Français
Facteur de puissance — ● Facteur de puissance rapport de la puissance active, exprimée en watts, à la puissance apparente, exprimée en voltampères … Encyclopédie Universelle
facteur de puissance — galios koeficientas statusas T sritis automatika atitikmenys: angl. power factor vok. Leistungsfaktor, m rus. коэффициент мощности, m pranc. facteur de puissance, m … Automatikos terminų žodynas
facteur de puissance — galios faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, lygus aktyviosios ir pilnutinės galios dalmeniui. atitikmenys: angl. power factor vok. Leistungsfaktor, m; Wirkfaktor, m rus. коэффициент мощности, m pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
facteur de puissance — galios faktorius statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, skaitine verte lygus kintamosios elektros srovės elektros energijos imtuvo aktyviosios galios ir pilnutinės galios dalmeniui. atitikmenys: angl. power factor vok … Penkiakalbis aiškinamasis metrologijos terminų žodynas
facteur de puissance — galios faktorius statusas T sritis fizika atitikmenys: angl. power factor vok. Leistungsfaktor, m; Wirkfaktor, m rus. фактор мощности, m pranc. facteur de puissance, m … Fizikos terminų žodynas
Correcteur du facteur de puissance — Le correcteur du facteur de puissance (anglais Power Factor Corrector, PFC) est un dispositif dans un appareil électrique, destiné à respecter les normes des fournisseurs d électricité sur le facteur de puissance. Un tel dispositif est… … Wikipédia en Français
appareil de mesure de facteur de puissance — galios faktoriaus matuoklis statusas T sritis Standartizacija ir metrologija apibrėžtis Elektrinės grandinės aktyviosios ir pilnutinės galios santykio matuoklis. atitikmenys: angl. cosφ meter; power factor meter vok. cosφ Anzeiger, m; cosφ Messer … Penkiakalbis aiškinamasis metrologijos terminų žodynas
mesureur de facteur de puissance — galios faktoriaus matuoklis statusas T sritis Standartizacija ir metrologija apibrėžtis Elektrinės grandinės aktyviosios ir pilnutinės galios santykio matuoklis. atitikmenys: angl. cosφ meter; power factor meter vok. cosφ Anzeiger, m; cosφ Messer … Penkiakalbis aiškinamasis metrologijos terminų žodynas
appareil de mesure de facteur de puissance — galios faktoriaus matuoklis statusas T sritis Standartizacija ir metrologija apibrėžtis Kintamosios įtampos ir srovės fazių skirtumo kosinuso matuoklis. atitikmenys: angl. cosφ meter; power factor meter vok. cosφ Anzeiger, m; cosφ Messer, m;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas

Dictionnaires et Encyclopédies sur 'Academic'

Facteur de puissance

Sommaire

Importance du facteur de puissance pour le distributeur