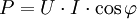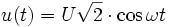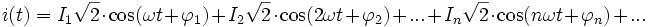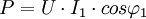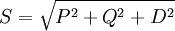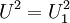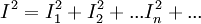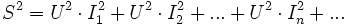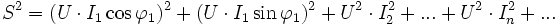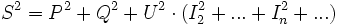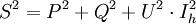Methode de Boucherot

Méthode de Boucherot

La méthode de Boucherot permet, en régime sinusoïdal de tension et de courant, de calculer la puissance totale consommée par une installation électrique comportant plusieurs dipôles électriques de facteur de puissance divers, ainsi que l'intensité totale appelée.

Cette méthode mise au point par Paul Boucherot, permet de faire des calculs selon un formalisme de type vectoriel sans utiliser la représentation de Fresnel trop lourde lorsque l'on est en présence de nombreux dipôles.

Utilité de la méthode

Dans le cadre d'une étude d'une installation, il faut calculer :

La puissance totale consommée: c’est ce que l’on paie.
L'intensité absorbée: pour le dimensionnement des câbles, disjoncteurs, sectionneur, … et choix de l’abonnement..
Le facteur de puissance global lorsque c'est utile (installations alimentées en haute tension, généralement industrielles).
La valeur des condensateurs s'il y' a lieu d'améliorer ce facteur de puissance.

Mise en œuvre

Pour chaque dipôle 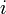$i \,$ on calcule 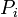$P_i \,$ et $Q_i \,$
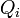
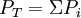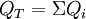L’installation consomme $P_T = \Sigma P_i \,$ et $Q_T = \Sigma Q_i \,$ .
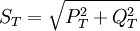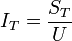On en déduit $S_T = \sqrt {P_T^2 + Q_T^2} \,$ , d’où l’intensité totale $I_T = \frac{S_T}{U} \,$ .

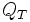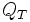En France, pour les installations alimentées en haute tension, la partie de puissance réactive $Q_T \,$ est gratuite à concurrence de $0,4 \cdot P_T \,$ (Décret n° 2002-1014 du 19 juillet 2002 ^[1]). L'excédent est facturé pendant les heures pleines des mois d'hivers. Il est parfois judicieux d'ajouter des condensateurs afin d’obtenir $Q_T \,$ final inférieur à $0,4 \cdot P_T \,$

Régimes sinusoïdaux monophasés

Il est rare que ces installations de faibles puissances nécessitent de faire des calculs de facteurs de puissance (sauf dans les exercices scolaires). Cependant il est parfois utile de pouvoir calculer l'intensité totale absorbée.

La puissance active est soit connue, indiquée par la plaque signalétique du récepteur, soit obtenue à l'aide de la relation :

$P = U \cdot I \cdot \cos \varphi \,$

D'autre part, on utilise les définitions des intermédiaires de calculs suivantes :

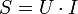La puissance apparente : $S = U \cdot I \,$ ,
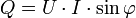La puissance réactive : $Q = U\cdot I \cdot \sin \varphi \,$ ,

puis on applique la méthode ci-dessus.

On peut, au cours des calculs, utiliser les relations suivantes :

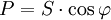$P = S \cdot \cos \varphi \,$ ,
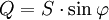$Q = S\cdot \sin \varphi \,$ ,
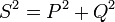
$S^2 = P^2 + Q^2 \,$
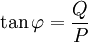
$\tan \varphi = \frac{Q}{P} \,$

Régimes sinusoïdaux triphasés

La méthode s'applique de la même manière mais on utilise les relations suivantes avec la racine de 3 qui vaut 1,732:

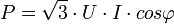
Puissance active: $P = \sqrt {3} \cdot U \cdot I \cdot cos \varphi \,$
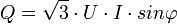
Puissance réactive : $Q =\sqrt {3} \cdot U\cdot I \cdot sin \varphi \,$
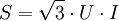
Puissance apparente : $S = \sqrt {3} \cdot U \cdot I \,$

Installations alimentées en tension sinusoïdale et absorbant des courants non sinusoïdaux

Dans le cas où le courant absorbé n'est pas sinusoïdal, le problème est plus complexe : même si le courant est en phase avec la tension, la puissance n'est pas égale au produit des valeurs efficaces

La tension, sinusoïdale, peut s'écrire

$u(t) = U \sqrt{2} \cdot \cos \omega t \,$

Le courant, non sinusoïdal, peut se décomposer en série, dite série de Fourier :

$i(t) = I_1 \sqrt{2} \cdot \cos (\omega t + \varphi_1) + I_2 \sqrt{2} \cdot \cos (2\omega t + \varphi_2) + ... + I_n \sqrt{2} \cdot \cos (n\omega t + \varphi_n) + ... \,$

Le calcul de la puissance active donne comme résultat :

$P = U \cdot I_1 \cdot cos \varphi_1 \,$

D'autre part la puissance apparente 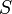$S \,$ peut s'écrire :

$S =\sqrt { P^2 + Q^2 +D^2} \,$

Avec les définitions des intermédiaires de calcul suivants :

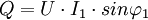
La puissance réactive : $Q = U \cdot I_1 \cdot sin \varphi_1 \,$
La puissance déformante: 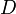$D \,$ telle que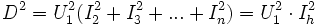 $D^2 = U_1^2 (I_2^2 + I_3^2 + ... + I_n^2 ) = U_1^2 \cdot I_h^2 \,$

et :

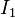$I_1 \,$ : la valeur efficace du fondamental du courant
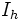$I_h \,$ : la valeur efficace de l'ensemble des harmoniques de rang supérieur à 1 du courant
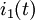$\varphi_1 \,$ : la valeur du déphasage du fondamental $i_1(t) \,$ par rapport à la tension.
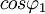$cos \varphi_1 \,$ : facteur de déplacement

Détail des calculs

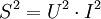
on a : $S^2 =U^2 \cdot I^2 \,$

avec :

$U^2 =U_1^2 \,$

$I^2 =I_1^2 +I_2^2 + ... I_n^2 + ... \,$

d'où :

$S^2 = U^2 \cdot I_1^2 + U^2 \cdot I_2^2+ ... + U^2 \cdot I_n^2+ ... \,$

$S^2 = (U\cdot I_1 \cos \varphi_1)^2 + (U\cdot I_1 \sin \varphi_1)^2 + U^2 \cdot I_2^2+ ... + U^2 \cdot I_n^2+ ... \,$

$S^2 = P^2 + Q^2 + U^2 \cdot ( I_2^2+ ... + I_n^2+ ...) \,$

$S^2 = P^2 + Q^2 + U^2 \cdot I_h^2 \,$

Notes et références

↑ Décret n° 2002-1014 du 19 juillet 2002 fixant les tarifs d'utilisation des réseaux publics de transport et de distribution d'électricité en application de l'article 4 de la loi n° 2000-108 du 10 février 2000 relative à la modernisation et au développement du service public de l'électricité

Articles connexes

Portail de l’électricité et de l’électronique

Ce document provient de « M%C3%A9thode de Boucherot ».

Catégories : Électrotechnique | Théorème de physique

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Methode de Boucherot de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Méthode De Boucherot — La méthode de Boucherot permet, en régime sinusoïdal de tension et de courant, de calculer la puissance totale consommée par une installation électrique comportant plusieurs dipôles électriques de facteur de puissance divers, ainsi que l… … Wikipédia en Français
Méthode de boucherot — La méthode de Boucherot permet, en régime sinusoïdal de tension et de courant, de calculer la puissance totale consommée par une installation électrique comportant plusieurs dipôles électriques de facteur de puissance divers, ainsi que l… … Wikipédia en Français
Méthode de Boucherot — La méthode de Boucherot permet, en régime sinusoïdal de tension et de courant, de calculer la puissance totale consommée par une installation électrique comportant plusieurs dipôles électriques de facteur de puissance divers, ainsi que l… … Wikipédia en Français
Théorème de Boucherot — Méthode de Boucherot La méthode de Boucherot permet, en régime sinusoïdal de tension et de courant, de calculer la puissance totale consommée par une installation électrique comportant plusieurs dipôles électriques de facteur de puissance divers … Wikipédia en Français
Boucherot — Paul Boucherot Paul Boucherot (1869 1943) a été ingénieur à la Compagnie des chemins de fer du nord. Elève de l École supérieure de physique et de chimie industrielles de la ville de Paris (4°), il a inventé la distribution électrique à courant… … Wikipédia en Français
Paul Boucherot — (1869 1943) a été ingénieur à la Compagnie des chemins de fer du nord. Élève de l École supérieure de physique et de chimie industrielles de la ville de Paris (4e promotion)[1], il a inventé la distribution électrique à courant constant, a fait… … Wikipédia en Français
Puissance (physique) — Pour les articles homonymes, voir Puissance. En physique, la puissance est la quantité d énergie par unité de temps fournie par un système à un autre. La puissance correspond donc à un débit d énergie : deux systèmes de puissances… … Wikipédia en Français
ESPCI — École supérieure de physique et de chimie industrielles de la ville de Paris ESPCI ParisTech Nom original École supérieure de physique et de chimie industrielles de la ville de Paris Informations Fondation 1882 Type … Wikipédia en Français
ESPCI ParisTech — École supérieure de physique et de chimie industrielles de la ville de Paris ESPCI ParisTech Nom original École supérieure de physique et de chimie industrielles de la ville de Paris Informations Fondation 1882 Type … Wikipédia en Français
Ecole Supérieure de Physique et de Chimie Industrielles — École supérieure de physique et de chimie industrielles de la ville de Paris ESPCI ParisTech Nom original École supérieure de physique et de chimie industrielles de la ville de Paris Informations Fondation 1882 Type … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Methode de Boucherot

Méthode de Boucherot

Sommaire

Utilité de la méthode