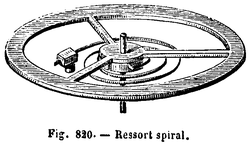
Ressort spiral

Le ressort spiral type, à spires non jointives et donc sans frottement, est composé d'un ruban de section rectangulaire encastré à une extrémité B et solidaire à l'autre extrémité 0 d'un axe perpendiculaire au plan d'enroulement.

Balancier avec ressort spiral

En horlogerie, le ressort spiral est un petit ressort enroulé en spirale et constituant avec le balancier l'organe réglant de la montre mécanique. Il ramène le balancier à sa position de départ à la fin de chaque alternance.

Nous supposerons que l'axe est mobile sans frottement et, ce qui est moins évident, qu'il ne tend pas à se déplacer radialement lorsqu'on le fait tourner sous l'effet d'un couple C.

Dans ces conditions, tout couple perpendiculaire au plan d'enroulement, appliqué en O, se trouve transmis intégralement en B, ce qui ne serait pas le cas si en ce point l'extrémité n'était pas encastrée mais simplement accrochée, comme ce sera probablement le cas pour cette réalisation industrielle :

Condition de résistance

Si la lame élastique a pour largeur b (comptée perpendiculairement au plan d'enroulement) et pour épaisseur e, alors :

Condition de déformation

Pour une poutre soumise à la flexion, une variation du moment fléchissant entraîne une variation de la courbure (inverse du rayon de courbure), telle que :

L'intégration sur l'ensemble de la longueur L du ruban fournit l'angle de rotation θ de l'extrémité O :

(θ est en radians)

En éliminant C entre les deux formules, il vient :

Fabrication

Le ressort spiral, essentiellement utilisé dans l'appareillage de précision (montres, appareils électriques, ...) fait l'objet d'une fabrication très spéciale dont les modes opératoires et les essais sont codifiés par le Centre Technique de l'Industrie Horlogère. L'obtention de spires non jointives et équidistantes nécessite, au départ, une conformation spéciale du ruban. Ce dernier, s'il était droit au départ, se disposerait en effet naturellement sous la forme d'un rouleau à spires jointives de comportement très différent à cause des frottements. On trouve une telle disposition dans le cas des ressorts qui rappellent les mètres à ruban dans leur boîtier.

Lorsque les extrémités du ressort spiral sont liées normalement, c'est-à-dire encastrées, toute variation du moment de flexion à l'une des extrémités est intégralement transmise à l'autre extrémité : ceci fait que dans tous les cas le moment de flexion le long du ruban est constant.

En un point donné, la courbure de la lame est définie comme l'inverse du rayon de courbure local. Or, comme la section de la lame est constante, toute variation du moment de flexion s'accompagne d'une variation proportionnelle de la courbure :

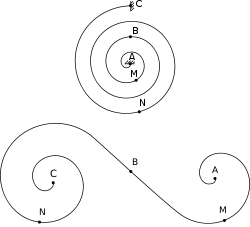
Nous conviendrons de dire que tout le long du ressort enroulé en charge, la courbure est positive. La figure ci-contre représente en haut un ressort spiral enroulé et au-dessous, à vide. Au niveau de l'extrémité intérieure A et du point M, la courbure de l'ébauche est positive et le reste après enroulement. Le point B correspond à un point d'inflexion de la préforme, où la courbure est nulle. Au point N et à l'extrémité extérieure C, les courbures de la préforme sont négatives et elles deviennent positives une fois le ressort enroulé.

La mise en forme du ressort « en S » à vide est une opération complexe qui demande beaucoup de savoir-faire et d'expérience !

Pour d'autres types de ressorts spiraux comme ceux des balanciers utilisés en horlogerie, la forme à vide est une spirale d'Archimède dont les courbures augmentent ou diminuent au gré des oscillations. En réglant la longueur du ruban flexible par un dispositif approprié, on fait varier la raideur du ressort et donc la fréquence des oscillations du balancier, on réduit ainsi autant que faire se peut l'avance ou le retard de la montre ou de la pendule.

Plus que tout autre, le ressort spiral est une affaire de spécialistes !

Montage

Nous avons supposé que l'extrémité du ressort était encastrée et affirmé que dans ces conditions le couple transmis par la lame était identique en tout point de cette dernière. Si par contre l'extrémité du ressort est simplement accrochée en C, le moment est nul en ce point et variable tout au long du ruban, avec un maximum atteignant presque 2C !

Le mode de fixation influe donc énormément sur la contrainte maximale.

Histoire

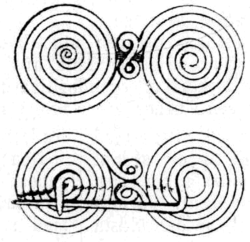Fibule ancienne à ressort spiralé

Le ressort spiralé a été inventé dès l'Antiquité, probablement par hasard après trempage d'un fil de fer ou de bronze enroulé en spirale ou double spirale inversée. Cette forme de ressort a par exemple été utilisé pour la fermeture des fibules qui jouaient le rôle d'épingle de sûreté. On le retrouve dans les serrures du Moyen Âge, puis plus tard pour animer les mécanismes de montres à ressort spiralé.

Voir aussi

Articles connexes

• assortiments
• balancier
• Composition d'une montre mécanique

• Portail de la physique
• Portail de l’horlogerie