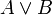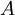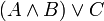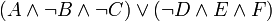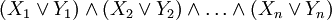FND

En logique booléenne ou en Calcul des propositions, une forme normale disjonctive (FND) est une normalisation d'une expression logique qui est une disjonction de clauses conjonctives. Elle est utilisée dans la démonstration automatique de théorèmes. Une expression logique est en FND si et seulement si elle est une disjonction d'une ou plusieurs conjonctions d'un ou plusieurs littéraux. Tout comme dans une forme normale conjonctive (FNC), les seuls opérateurs dans une FND sont le et logique, le ou logique et la négation. L'opérateur non ne peut être utilisé que dans un littéral, c'est-à-dire qu'il ne peut que précéder une variable. Par exemple, toutes les expressions suivantes sont en FND:

Cependant, les expressions suivantes ne sont pas en FND:

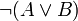— la négation s'applique à toute la parenthèse plutôt que directement à une variable

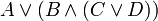— un ou est imbriqué dans un et

Convertir une expression vers une FND requiert l'utilisation d'équivalences logiques, comme l'élimination de double négations, les lois de De Morgan, et la loi de distributivité. Toutes les expressions booléennes peuvent être converties en FND. Cependant, dans quelques cas la conversion à la FND peut mener à un allongement exponentiel de l'expression. Par exemple, la FND d'une expression de la forme suivante a 2ⁿ termes :

Ce qui suit est une grammaire formelle pour la FND :

1. <ou> → ∨
2. <et> → ∧
3. <non> → ¬
4. <disjonction> → <conjonction>
5. <disjonction> → <disjonction> <ou> <conjonction>
6. <conjonction> → <littéral>
7. <conjonction> → (<conjonction> <et> <littéral>)
8. <littéral> → <terme>
9. <littéral> → <non><terme>

où <terme> est une variable quelconque.

Articles connexes

• Forme normale conjonctive
• Forme normale algébrique
• Fonction booléenne
• Clause de Horn
• Calcul des propositions
• Algorithme de Quine–McCluskey
• Table de vérité
• Littéral (logique)

• Portail de la logique
• Portail des mathématiques