Expérience de Cavendish

Expérience de Cavendish

L'expérience de Cavendish, avait pour but initial de pouvoir estimer la masse de la Terre. Cette dernière étant directement liée, dans l'équation de Newton, à la constante de gravitation, l'expérience permet de déterminer cette constante.

Le physicien britannique Henry Cavendish réalisa cette expérience à la fin du XVIIIe siècle à l'aide d'une balance de torsion.

Sommaire

Historique

Schéma d'une balance de torsion

L'un des premiers essais de détermination de la masse de la Terre fut effectué par le géophysicien Pierre Bouguer. Lorsqu'il se trouvait au Pérou, il tenta de mesurer, en vain, le faible déplacement d'un fil à plomb à proximité d'un volcan. Les déviations étant trop faibles, il lui fut impossible d'obtenir un résultant convaincant. En ce qui le concerne, Bouguer voulait mesurer la densité de la Terre.

Cette même méthode fut reprise par deux anglais en 1755 : Nevil Maskelyne et Charles Hutton. Leur expérience eut lieu près d'une montagne en Ecosse et fut concluante. Ils estimèrent la masse volumique de la Terre entre 4,5 et 5 grammes par centimètres cubes.

C'est en 1798 que Cavendish, continuant les travaux de John Michelle, utilisa un système autre, la balance de torsion, afin de déterminer précisément cette masse volumique.

Balance de torsion

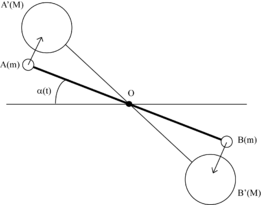
Le principe de la balance de torsion est simple. Il s'agit d'obtenir un système qui établit l'équilibre entre la force de torsion d'un fil et la force d'attraction gravitationnelle. Lorsque l'on écarte le système des deux sphères de sa position d'équilibre d'un angle θ alors celles-ci, afin de retrouver l'état d'équilibre, oscillent autour de leur position d'équilibre (oscillations amorties).

Afin d'intégrer le paramètre d'attraction gravitationnelle, on utilise un second système de sphères, fixes, et de masse beaucoup plus importante. Alors le système va entrer en oscillation lui permettant ainsi de s'équilibrer en fonction de la force d'attraction et de la force de rappel.

Constante de gravitation

Notations

On note r la distance entre une petite masse m et le point O. r est donc une constante.

On note d la distance entre une petite masse m et une grosse masse M directement voisine. d est une fonction du temps.

Calcul

Afin de déterminer la constante G on va considérer diverses interactions entre les éléments du système :

  • les frottements de l'air
  • les interactions A-A' et B-B'
  • la force de torsion du fil

On négligera les forces d'interactions A-B' et A'-B, puisqu'elles sont nettement plus faibles.

On va à présent utiliser le théorème du moment cinétique :

\frac{\mathrm d\overrightarrow{L_O}}{\mathrm dt} = \sum_{i=1}^{n} \overrightarrow{\mathcal M_{i,O}}

Ici le moment cinétique s'écrit :

{L_0}=I \dot{\alpha}

avec

I=\sum_{i} m_i r_i^2=2 m r^2

Le pendule est soumis à trois moments de force:

\mathcal M_{i,0}^{rappel} = - C \alpha

  • Le moment du couple d'amortissement visqueux

\mathcal M_{i,0}^{frott} = - K \dot{\alpha}

  • Le moment du couple de forces A'-A et B'-B

\mathcal M_{i,0}^{\overrightarrow{F_{A'-A}}}+ \mathcal M_{i,0}^{\overrightarrow{F_{B'-B}}} = 2 G \frac{m M}{d^2} r

Le théorème du moment cinétique devient donc :

2 m r^2 \ddot{\alpha} + K \dot{\alpha} + C \alpha = 2 G \frac{m M}{d^2} r

qui est l'équation différentielle du mouvement du pendule en régime oscillatoire forcé.

Lorsque l'on relâche le système celui-ci finit par osciller très peu autour de sa position d'équilibre. On peut donc dire que lorsque le temps tend vers l'infini, les oscillations sont relativement faibles, d'où l'approximation suivante :

\alpha_{final} \approx Cte \Rightarrow \dot{\alpha}_{final} \rightarrow 0 \Rightarrow \ddot{\alpha}_{final} \rightarrow 0

ce qui donne la solution particulière de l'équation différentielle :

\alpha_{final} = 2 \frac{G m M}{d^2} \frac{r}{C}

G = \frac{C d^2 \alpha_{final}}{2 m M r}

Erreurs d'approximation

Jusqu'alors, on avait supposé que l'interaction entre les sphères A'-B et B'-A étaient négligeables. Cela dépend en fait du rapport de distance qu'il y a entre la grosse sphère voisine et la grosse sphère éloignée. En supposant qu'il y a un rapport r dans ces distances alors on peut démontrer que l'erreur sur G est de la forme :

\epsilon = {\left( 1 - \frac{\sin{\theta}}{r} \right)}^2

avec

\theta = \widehat{BAB'}

En pratique, on obtient une erreur relativement faible pour r > 10 (les valeurs sont données comme incertitude sur G):

  • r=5 \epsilon = 20,6%
  • r=10 \epsilon = 9,6%
  • r=20 \epsilon = 4,6%
  • r=50 \epsilon = 1,8%

Résultats de Cavendish

Lorsqu'il effectua ses mesures, Cavendish obtint de très bons résultats. Voici ses résultats en comparaison avec les valeurs communément admises :

G_{Cavendish} = \ 6,754 \ 10^{-11} \ N \ m^2 \ kg^{-2}

G_{reel} = \ 6,674 \ 10^{-11} \ N \ m^2 \ kg^{-2}

M_{Cavendish} = \ 5.980 \ 10^{24} \ kg

M_{reel} = \ 5.974 \ 10^{24} \ kg

d_{Cavendish} = \ 5.48 \ g \ cm^{-3}

d_{reel} = \ 5.54 \ g \ cm^{-3}

Voir aussi


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Expérience de Cavendish de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Experience de Cavendish — Expérience de Cavendish L expérience de Cavendish, avait pour but initial de pouvoir estimer la masse de la Terre. La masse de la Terre étant directement liée, dans l équation de Newton, à la constante de gravitation, l expérience permet de… …   Wikipédia en Français

  • expérience de Cavendish — Kevendišo eksperimentas statusas T sritis fizika atitikmenys: angl. Cavendish experiment vok. Cavendishscher Versuch, m rus. опыт Кавендиша, m pranc. expérience de Cavendish, f …   Fizikos terminų žodynas

  • Expérience du Schiehallion — Masse de la Terre La masse M de la Terre est estimée à 5,9736 x 1024 kg. Elle est obtenue à partir de la connaissance très précise fournie par la géodésie spatiale de la constante géocentrique GM et de la connaissance beaucoup moins précise… …   Wikipédia en Français

  • Cavendish experiment — Kevendišo eksperimentas statusas T sritis fizika atitikmenys: angl. Cavendish experiment vok. Cavendishscher Versuch, m rus. опыт Кавендиша, m pranc. expérience de Cavendish, f …   Fizikos terminų žodynas

  • CAVENDISH (H.) — En découvrant la composition élémentaire de l’eau, et en précisant celle de l’air, Cavendish a rompu de façon décisive le cercle dans lequel sensation et représentation étaient enfermées depuis l’Antiquité. C’est dans son œuvre que les éléments… …   Encyclopédie Universelle

  • Henry Cavendish — Pour les articles homonymes, voir Cavendish. Henry Cavendish. Henry Cavendish (10 octobre 1731, Nice …   Wikipédia en Français

  • Margaret Cavendish — See Margaret Cavendish (1661 1717) for the later Duchess of Newcastle of this name. Margaret Cavendish, Duchess of Newcastle upon Tyne (1623 ndash; 15 December 1673), was an English aristocrat and a prolific writer. Born Margaret Lucas, she was… …   Wikipedia

  • Margaret Cavendish, Duchess of Newcastle-upon-Tyne — Margaret Cavendish Segment from Frontispiece for several of her books in the 1650s and 1660s …   Wikipedia

  • Victor Cavendish, 9th Duke of Devonshire — Victor Christian William Cavendish, 9th Duke of Devonshire, KG, GCMG, GCVO (London May 31, 1868 – May 6, 1938 Chatsworth House), was a Liberal Unionist Member of Parliament for West Derbyshire (1891–1908), Governor General of Canada (1916–1921),… …   Wikipedia

  • Michael Robert Cavendish — Legal Ethics Writer/Theorist Michael Cavendish Born 1972 …   Wikipedia

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”