Espace precompact
- Espace precompact
-
Espace précompact
Un espace métrique E est précompact si pour tout ε > 0, on peut recouvrir E par un nombre fini de boules ouvertes de rayons  .
.
- Proposition 1 : Soit E un espace métrique compact ; alors E est précompact.
- Démonstration :
- Soit
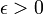 , alors,
, alors, 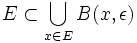
- Comme une boule ouverte est un ouvert et que E est compact, on peut extraire de ce recouvrement de E par des ouverts un sous recouvrement fini, d'où le résultat.
- Proposition 2 : Soit E un espace métrique complet et précompact, alors E est compact.
- Démonstration :
- On va montrer que E vérifie la propriété de Bolzano-Weierstrass qui est équivalente à Borel-Lebesgue dans les espaces métriques.
- Soit x une suite de E. Recouvrons E par un nombre fini n(0) de boules ouvertes de rayon 20 = 1 :
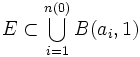 .
.
- Une de ces boules contient une infinité I(0) de termes de la suite, appelons-la B0.
- Mais on peut aussi recouvrir E par un nombre n(1) de boules ouvertes de rayon 2 − 1.
- Dans ce cas, il existe une boule B1, de rayon2 − 1, contenant une partie infinie I(1) de I(0)
- (si ce n'était le cas, toute boule B(ai,2 − 1) ne contiendrait qu'un nombre fini d'éléments de I(0), et donc E également, ce qui est absurde)
- on peut itérer le procédé pour obtenir
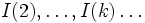 une suite décroissante de parties infinies et de diamètres tendant vers 0 (car majorés par 2 − k + 1)
une suite décroissante de parties infinies et de diamètres tendant vers 0 (car majorés par 2 − k + 1)
- Ainsi, obtient une sous-suite de x, et qui est de Cauchy.
- Par complétude, celle-ci converge dans E.

 Portail des mathématiques
Portail des mathématiques
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Espace precompact de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Espace Précompact — Un espace métrique E est précompact si pour tout ε > 0, on peut recouvrir E par un nombre fini de boules ouvertes de rayons . Proposition 1 : Soit E un espace métrique compact ; alors E est précompact. Démonstration : Soit ,… … Wikipédia en Français
Espace précompact — En topologie, une branche des mathématiques, un espace métrique E est précompact si pour tout ε>0, on peut recouvrir E par un nombre fini de boules ouvertes de rayon ε, ou de façon équivalente si pour tout ε>0, on peut recouvrir E par un… … Wikipédia en Français
Précompact — Espace précompact Un espace métrique E est précompact si pour tout ε > 0, on peut recouvrir E par un nombre fini de boules ouvertes de rayons . Proposition 1 : Soit E un espace métrique compact ; alors E est précompact.… … Wikipédia en Français
Espace Séparable — En mathématiques, et plus précisément en topologie, un espace séparable est un espace topologique contenant un sous ensemble dénombrable et dense, c est à dire si l on peut trouver un ensemble dénombrable de points dont l adhérence est égale à l… … Wikipédia en Français
Espace separable — Espace séparable En mathématiques, et plus précisément en topologie, un espace séparable est un espace topologique contenant un sous ensemble dénombrable et dense, c est à dire si l on peut trouver un ensemble dénombrable de points dont l… … Wikipédia en Français
Espace Complet — En mathématiques, un espace métrique M est dit complet ou espace complet si toute suite de Cauchy de M a une limite dans M (c’est à dire qu elle converge dans M). La propriété de complétude dépend de la distance. Il est donc important de toujours … Wikipédia en Français
Espace séparable — Ne pas confondre avec la structure d espace séparé. En mathématiques, et plus précisément en topologie, un espace séparable est un espace topologique contenant un sous ensemble fini ou dénombrable et dense, c est à dire contenant un… … Wikipédia en Français
Espace complet — En mathématiques, un espace métrique M est dit complet ou espace complet si toute suite de Cauchy de M a une limite dans M (c’est à dire qu elle converge dans M). La propriété de complétude dépend de la distance. Il est donc important de toujours … Wikipédia en Français
Complété d'un espace — Espace complet En mathématiques, un espace métrique M est dit complet ou espace complet si toute suite de Cauchy de M a une limite dans M (c’est à dire qu elle converge dans M). La propriété de complétude dépend de la distance. Il est donc… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
 .
.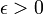 , alors,
, alors, 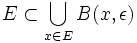
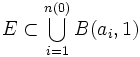 .
.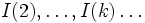 une suite décroissante de parties infinies et de diamètres tendant vers 0 (car majorés par 2 − k + 1)
une suite décroissante de parties infinies et de diamètres tendant vers 0 (car majorés par 2 − k + 1)
