Espace de compactification

Espace de compactification

Réduction dimensionnelle

En physique, une réduction dimensionnelle est une procédure par laquelle, étant donnée une théorie formulée sur un espace-temps 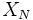X_N\, de dimension 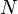N\,, on construit une autre théorie formulée sur un sous-espace 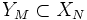Y_M\subset X_N\, de dimension 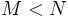M<N\, . Dans la suite nous allons décrire brièvement plusieurs procédures de réduction communément utilisées.

Sommaire

Réduction de Kaluza-Klein

Article détaillé : théorie de Kaluza-Klein.

Dans cette approche, la plus simple, on contraint les champs de la théorie en 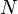N\, dimensions à ne dépendre que des 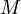M\, coordonnées du sous-espace 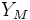Y_M\,. Par exemple si on considère 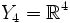Y_4=\mathbb{R}^4\,, c'est-à-dire l'espace de Minkowski et 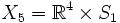X_5=\mathbb{R}^4\times S_1\,, on parle de réduction sur un cercle et le cercle est appelé espace de compactification. Dans ce cas on contraint les champs à ne pas dépendre de la coordonnée angulaire sur le cercle. C'est le cadre historiquement considéré par Theodor Kaluza et Oskar Klein dans le contexte de la relativité générale à 5 dimensions pour tenter de reproduire la théorie de l'électromagnétisme et son invariance de jauge en 4 dimensions à partir de l'invariance par reparamétrisation de la théorie originale à 5 dimensions. Par usage, la généralisation de cette réduction dimensionnelle à d'autres espaces est alors communément appelée également réduction de Kaluza-Klein. 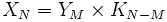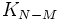Si on peut écrire X_N=Y_M\times K_{N-M}\, avec K_{N-M}\, une variété compacte de dimension 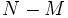N-M\, alors on continue à appeler 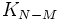K_{N-M}\, l'espace de compactification et on dit qu'on effectue une réduction sur 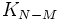K_{N-M}\,[1].

Si la théorie originale possède des équations du mouvement issues d'une action 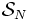\mathcal{S}_N\, alors il est nécessaire de s'assurer que la restriction imposée aux champs de ne dépendre que des coordonnées de 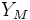Y_M\, est compatible avec les équations du mouvements, c'est-à-dire que les champs restreints sont encore des solutions des équations du mouvement. On parle alors dans ce cas de troncation consistante. Les réductions sur des tores ou réductions toroïdales sont toujours consistantes. Pour des variétés de compactification plus compliquées(comme des sphères par exemple) la réponse n'est pas évidente et demande une analyse au cas par cas.

Réduction de Scherk-Schwarz

Les champs ne sont pas indépendants des coordonnées de 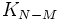K_{N-M}\, mais leur dépendance est simple et dépend des symétries de la théorie originale.

Notes

  1. ↑ On peut considérer en fait le cas plus général où X_N\, est une fibration sur Y_M\, de fibre K_{N-M}\,.

Voir aussi

  • Portail de la physique Portail de la physique
Ce document provient de « R%C3%A9duction dimensionnelle ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espace de compactification de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Espace K3 — K3 (géométrie) Pour les articles homonymes, voir K3. En géométrie différentielle ou algébrique, l espace K3, ou encore la surface K3, est la variété de Calabi Yau de plus petite dimension différent d un tore. C est une variété complexe de… …   Wikipédia en Français

  • Espace de Calabi-Yau — Variété de Calabi Yau Un exemple de variété de Calabi Yau Une variété de Calabi Yau, ou espace de Calabi Yau est un type particulier de variété en mathématiques intervenant dans des domaines comme la géométrie algébrique mais également en… …   Wikipédia en Français

  • Compactification (Mathématiques) — En topologie, la compactification est un procédé général de plongement d un espace topologique comme sous espace dense d un espace compact. Le plongement est appelé le compactifié. L existence d un tel plongement implique que l espace doit être… …   Wikipédia en Français

  • Compactification (mathematiques) — Compactification (mathématiques) En topologie, la compactification est un procédé général de plongement d un espace topologique comme sous espace dense d un espace compact. Le plongement est appelé le compactifié. L existence d un tel plongement… …   Wikipédia en Français

  • Espace Localement Compact — En topologie, un espace localement compact est un espace qui, sans être nécessairement compact lui même, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de résultats sur les espaces… …   Wikipédia en Français

  • Espace De Modules — En mathématiques, un espace de modules est un espace paramétrant les diverses classes d objets sous une relation d équivalence ; l intérêt est de pouvoir alors munir naturellement ces espace de classes d une structure supplémentaire. L… …   Wikipédia en Français

  • Compactification de Stone–Čech — En mathématiques, et plus précisément en topologie générale, la compactification de Stone–Čech (découverte en 1937 par Marshall Stone (en)[1] et Eduard Čech[2]) est une technique de construction d un espace com …   Wikipédia en Français

  • Compactification (mathématiques) — En topologie, la compactification est un procédé général de plongement d un espace topologique comme sous espace dense d un espace compact. Le plongement est appelé le compactifié. L existence d un tel plongement implique que l espace doit être… …   Wikipédia en Français

  • Compactification d'Alexandrov — Compactifié d Alexandroff Soit X un espace topologique séparé et localement compact, mais non compact. On peut, en ajoutant un point à X, obtenir un espace compact. Pour cela, on considère où , et on définit une topologie de la manière suivante.… …   Wikipédia en Français

  • Espace localement compact — En topologie, un espace localement compact est un espace séparé qui, sans être nécessairement compact lui même, admet des voisinages compacts pour tous ses points. On peut y généraliser (au moins partiellement) beaucoup de résultats sur les… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”