Espace d'Euler

Espace d'Euler

Angles d'Euler

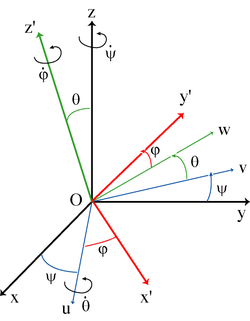
Page d'aide sur l'homonymie Pour les articles homonymes, voir Euler.

Le mouvement d'un solide par rapport à un référentiel fait intervenir 6 paramètres, qui sont, par exemple, les trois coordonnées décrivant la position de son centre de masse (ou d'un point quelconque du solide) et trois angles, nommés les angles d'Euler, cf. le schéma ci-contre. Les angles d'Euler peuvent aussi servir à représenter l'orientation d'un solide par rapport à un repère ; on peut les voir comme une généralisation des coordonnées sphériques.

Sommaire

Mécanique du solide

Angles d'Euler

On s'intéresse seulement ici à la description du mouvement du solide en rotation quelconque autour du point O, qui peut être un point fixe du solide dans le référentiel de référence Oxyz ou le centre de masse.

Les angles d'Euler sont choisis de façon à permettre une mémorisation simple de la construction du vecteur rotation instantané du solide, nécessaire à l'étude de la cinématique du solide.

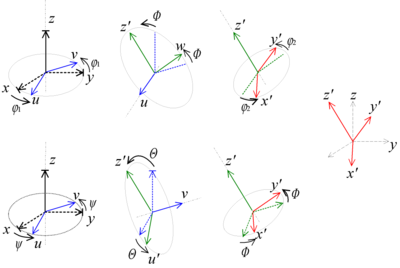
On passe du référentiel fixe Oxyz au référentiel lié au solide Ox'y'z' par trois rotations successives.

  • La précession ψ, autour de l'axe Oz, fait passer de Oxyz au référentiel Ouvz.
  • La nutation θ, autour de l'axe Ou, fait passer de Ouvz à Ouwz'.
  • La rotation propre \varphi, autour de l'axe Oz', fait passer de Ouwz’ au référentiel lié au solide Ox'y'z’.

NB. L'axe Ou est porté par l'intersection des plans Oxy et Ox'y'

Dans ces conditions le vecteur rotation instantané du solide est donné par la simple somme :

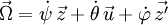\vec{\Omega} =\dot{\psi}\,\vec{z}+\dot{\theta}\,\vec{u}+\dot{\varphi}\,\vec{z'},

où les vecteurs apparaissant dans le membre de droite sont les vecteurs unitaires des axes correspondants. On remarquera que l'expression simple précédente utilise une base non orthogonale.

L'utilisation de ces angles est très générale en mécanique et en astronomie, par exemple pour décrire le mouvement du gyroscope.

Orientation cristalline

En science des matériaux, les angles d'Euler sont utilisés pour décrire l'orientation cristalline (orientation d'un cristallite par rapport aux axes de l'échantillon), notamment dans le domaine de la texture (orientation préférentielle). Les angles sont alors en général[1] notés (φ1,Φ,φ2) avec :

  • φ1 = ψ
  • Φ = θ
  • φ2 = φ

On utilise également parfois une autre variante dans laquelle la seconde rotation (nutation) se fait selon l'axe Ov au lieu de Ou ; les angles sont alors notés (Ψ,Θ,Φ) sans que cela ait un rapport avec les notations des mécaniciens, ce qui n'est pas sans risque de confusion.

Variantes des angles d'Euler

Notes

  1. ↑ il s'agit de la notation adoptée par Bunge dans son ouvrage Texture analysis in materials science, une référence dans le domaine

Voir également

Blocage de cardan

Lien externe

Une animation des angles d'Euler

  • Portail de la physique Portail de la physique
  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Angles d%27Euler ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espace d'Euler de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Espace Euclidien — En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le… …   Wikipédia en Français

  • Espace euclidien (algèbre linéaire) — Espace euclidien En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique …   Wikipédia en Français

  • EULER (L.) — Avec Joseph Louis Lagrange, son émule plus jeune, Leonhard Euler est l’un des deux géants mathématiques qui ont dominé la science du XVIIIe siècle. Ses travaux, d’une abondance inégalée, couvrent tout le champ des mathématiques, de la mécanique… …   Encyclopédie Universelle

  • ESPACE-TEMPS — La mécanique classique, sous la forme mathématique rigoureuse que lui a donnée Newton, repose sur les deux concepts fondamentaux d’espace et de temps absolus: un événement ponctuel est parfaitement déterminé lorsqu’on connaît sa position dans… …   Encyclopédie Universelle

  • Espace euclidien — En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le… …   Wikipédia en Français

  • Caractéristique d'Euler — En mathématiques, et plus précisément en géométrie et en topologie algébrique, la caractéristique d Euler ou d Euler Poincaré est un invariant numérique, un nombre qui décrit un aspect d une forme d un espace topologique ou de la structure de cet …   Wikipédia en Français

  • Caracteristique d'Euler — Caractéristique d Euler La caractéristique d Euler ou d Euler Poincaré est un invariant numérique, un nombre qui décrit un aspect d une forme de l espace topologique ou de la structure. Elle est communément notée par . La caractéristique d Euler… …   Wikipédia en Français

  • Caractéristique d'Euler-Poincaré — Caractéristique d Euler La caractéristique d Euler ou d Euler Poincaré est un invariant numérique, un nombre qui décrit un aspect d une forme de l espace topologique ou de la structure. Elle est communément notée par . La caractéristique d Euler… …   Wikipédia en Français

  • Quaternions et rotation dans l'espace — Les quaternions unitaires fournissent une notation mathématique commode pour représenter l orientation et la rotation d objets en trois dimensions. Comparés aux angles d Euler, ils sont plus simple à composer et évitent le problème du blocage de… …   Wikipédia en Français

  • Orientation dans l'espace — Pour les articles homonymes, voir Orientation. L orientation d un objet dans l espace est la manière dont est disposé cet objet, indépendamment de la position de son centre d inertie. Il faut pour cela fixer deux directions relatives à l objet.… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”