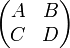Espace Stable Par Un Endomorphisme

Espace Stable Par Un Endomorphisme

Espace stable par un endomorphisme

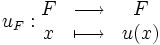
En algèbre linéaire, un endomorphisme laisse stable un sous espace vectoriel F quand les éléments de F ont pour image un élément de F.

La recherche de sous-espaces stables est étroitement liée à la théorie de la réduction des endomorphismes.

L'utilisation de sous-espaces stables permet de ramener des problèmes posés dans un espace de dimension n à des problèmes analogues en dimension inférieure, et éventuellement de mener à bien des démonstrations par récurrence.

Sommaire

Définitions

Soient E espace vectoriel et u endomorphisme de E.

Un sous-espace vectoriel F de E est dit stable quand 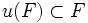u(F)\subset F. Dans ce cas u induit sur F un endomorphisme

u_F : \begin{matrix} F & \longrightarrow & F \\ x & \longmapsto & u(x)\end{matrix}

Il ne faut pas confondre cette notion avec celle de restriction d'un endomorphisme. La restriction est en effet définie que F soit stable ou non, mais est une application linéaire de F dans E.

Représentation matricielle

Si E est de dimension finie et muni d'une base adaptée à F (c'est-à-dire une base de F complétée en une base de E), la matrice représentative de u peut être notée par blocs

\begin{pmatrix} A&B\\C&D\end{pmatrix}

Alors F est un espace stable par u si et seulement si C=0, et dans ce cas la matrice de l'endomorphisme induit sur F est A.

Stabilité et trigonalisation

On suppose encore E de dimension finie n. Un endomorphisme est dit trigonalisable quand il possède une matrice représentative triangulaire supérieure.

Cela revient à chercher des espaces E_1\subset E_2\subset \dots \subset E_n=E, de dimensions respectives 1,2,..., n, tous stables par u. On parle alors de drapeau stable par u.

Propriétés

Droites et hyperplans stables

Une droite est stable par un endomorphisme si et seulement si elle est engendrée par un vecteur propre.

En dimension finie, un hyperplan est stable par l'endomorphisme u si et seulement s'il contient un espace de la forme Im(u − λId), ce qui ne peut se produire que pour λ valeur propre.

Dans un cadre euclidien, on peut donner une formulation duale : un hyperplan H est stable par l'endomorphisme u si et seulement si un vecteur normal à H est propre pour l'adjoint u*.

Commutation et stabilité

Si deux endomorphismes u et v commutent, tout espace propre pour l'un est stable par l'autre.

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Espace stable par un endomorphisme ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Espace Stable Par Un Endomorphisme de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Espace stable par un endomorphisme — En algèbre linéaire, un endomorphisme laisse stable un sous espace vectoriel F quand les éléments de F ont pour image un élément de F. La recherche de sous espaces stables est étroitement liée à la théorie de la réduction des endomorphismes. L… …   Wikipédia en Français

  • Sous-espace stable — En algèbre linéaire, un endomorphisme laisse stable un sous espace vectoriel F quand les éléments de F ont pour image un élément de F. La recherche de sous espaces stables est étroitement liée à la théorie de la réduction des endomorphismes.… …   Wikipédia en Français

  • Espace Vectoriel — En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée… …   Wikipédia en Français

  • Espace vectoriel linéaire — Espace vectoriel En algèbre linéaire, un espace vectoriel est une structure algébrique permettant en pratique d effectuer des combinaisons linéaires. Étant donné un corps (commutatif) K, un espace vectoriel E sur K est un groupe commutatif (dont… …   Wikipédia en Français

  • Espace propre — Valeur propre, vecteur propre et espace propre Fig. 1. Cette application linéaire déforme la statue de David. Les vecteurs bleus ont pour images les vecteurs verts. Ils gardent la même direction, ce sont des vecteurs propres. La valeur propre… …   Wikipédia en Français

  • Espace vectoriel — En algèbre linéaire, un espace vectoriel est un ensemble muni d une structure permettant d effectuer des combinaisons linéaires. Étant donné un corps K, un espace vectoriel E sur K est un groupe commutatif (dont la loi est notée +) muni d une… …   Wikipédia en Français

  • Endomorphisme nilpotent — Exemple d image d une base par un endomorphisme nilpotent en dimension 3. Un endomorphisme nilpotent est un morphisme d un objet mathématique sur lui même, qui, composé par lui même un nombre suffisant de fois, donne le morphisme nul. C’est donc… …   Wikipédia en Français

  • Endomorphisme normal — Un endomorphisme normal est un opérateur d un espace de Hilbert qui commute avec son adjoint. Sommaire 1 Définition 2 Exemples 3 Propriétés 4 Article connexe …   Wikipédia en Français

  • Reduction d'endomorphisme — Réduction d endomorphisme En mathématiques, et plus particulièrement en algèbre linéaire, la réduction d endomorphisme est une technique mathématique qui a pour objectif d exprimer des matrices et des endomorphismes sous une forme plus simple,… …   Wikipédia en Français

  • Réduction d'endomorphisme — En mathématiques, et plus particulièrement en algèbre linéaire, la réduction d endomorphisme est une technique mathématique qui a pour objectif d exprimer des matrices et des endomorphismes sous une forme plus simple, notamment pour faciliter les …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”