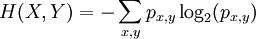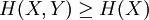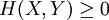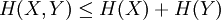Entropie Conjointe

Entropie conjointe

L'Entropie conjointe est une mesure d'entropie utilisée en théorie de l'information. L'entropie conjointe mesure combien d'information est contenue dans un système de deux variables aléatoires. Comme les autres entropies, l'entropie conjointe peut être mesuré en bits ou en nats, selon la base du logarithme utilisée.

Définition

Si chaque paire d'états possibles $(x, y)$ des variables aléatoires $(X, Y)$ ont une probabilité $p x, y$ alors l'entropie conjointe est définie par :

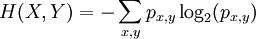
$H(X,Y) = -\sum_{x,y} p_{x,y} \log_2(p_{x,y}) \!$

Propriétés

L'entropie conjointe est supérieure ou égale à l'entropie d'une seule variable :

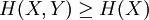
$H(X,Y) \geq H(X)$

Nous avons toujours l'entropie conjointe positive ou nulle :

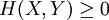
$H(X,Y) \geq 0$

Deux systèmes considérés ensemble ne peuvent pas apporter plus d'information que la somme des apports d'information de chacun :

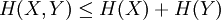
$H(X,Y) \leq H(X) + H(Y)$

avec égalité si X et Y sont des variables aléatoires indépendantes.

Voir aussi

Ce document provient de « Entropie conjointe ».

Catégorie : Théorie de l'information

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Entropie Conjointe de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Entropie conjointe — L Entropie conjointe est une mesure d entropie utilisée en théorie de l information. L entropie conjointe mesure combien d information est contenue dans un système de deux variables aléatoires. Comme les autres entropies, l entropie conjointe… … Wikipédia en Français
Entropie Conditionnelle — L entropie conditionnelle est une mesure d entropie utilisée en théorie de l information. L entropie conditionnelle mesure l entropie restante provenant de la variable aléatoire Y, si l on connait parfaitement la seconde variable aléatoire X. C… … Wikipédia en Français
Entropie conditionnée — Entropie conditionnelle L entropie conditionnelle est une mesure d entropie utilisée en théorie de l information. L entropie conditionnelle mesure l entropie restante provenant de la variable aléatoire Y, si l on connait parfaitement la seconde… … Wikipédia en Français
Entropie conditionnelle — L entropie conditionnelle est une mesure d entropie utilisée en théorie de l information. L entropie conditionnelle mesure l entropie restante provenant de la variable aléatoire Y, si l on connait parfaitement la seconde variable aléatoire X. C… … Wikipédia en Français
Entropie de Shannon — L entropie de Shannon, due à Claude Shannon, est une fonction mathématique qui, intuitivement, correspond à la quantité d information contenue ou délivrée par une source d information. Cette source peut être un texte écrit dans une langue donnée … Wikipédia en Français
Entropie croisée — Traduction à relire Cross entropy → Entropie c … Wikipédia en Français
Information Mutuelle — Dans la théorie des probabilités et la théorie de l information, l information mutuelle de deux variables aléatoires est une quantité mesurant la dépendance statistique de ces variables. Elle se mesure souvent en bit. L information mutuelle d un… … Wikipédia en Français
Information mutuelle — Dans la théorie des probabilités et la théorie de l information, l information mutuelle de deux variables aléatoires est une quantité mesurant la dépendance statistique de ces variables. Elle se mesure souvent en bit. L information mutuelle d un… … Wikipédia en Français
Stephane Lupasco — Stéphane Lupasco Stéphane Lupasco (en roumain Ştefan Lupaşcu ; 1900 1988) est un philosophe français d origine roumaine, auteur de la Logique dynamique du Contradictoire, fondée notamment sur la notion de Tiers inclus. Cette logique générale … Wikipédia en Français
Stéphane Lupasco — Pour les articles homonymes, voir Lupașcu. Stéphane Lupasco (en roumain Ștefan Lupașcu ; 1900 1988) est un philosophe français d origine roumaine, auteur de la Logique dynamique du Contradictoire, fondée notamment sur la notion de Tiers… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Entropie Conjointe