Entrelacs brunnien
- Entrelacs brunnien
-
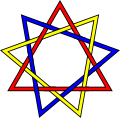
Ce nœud à quatre brins est un entrelacs brunnien.
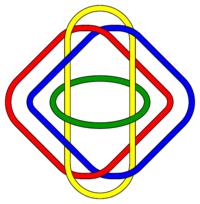
Entrelacs brunnien à six composants.
En théorie des nœuds, un entrelacs brunnien est un entrelacs non trivial qui devient trivial si l'un quelconque de ses composants est enlevé. En d'autres termes, couper n'importe laquelle des boucles libère toutes les boucles de l'entrelacs. L'adjectif brunnien vient de Hermann Brunn, qui a rédigé un article en 1892 prenant pour exemples de tels nœuds.
L'entrelacs brunnien le plus simple et le plus connu est le nœud borroméen, un entrelacs de trois éléments non noués entre eux. À partir de trois éléments, il existe une infinité d'entrelacements possibles contenant le même nombre de boucles. Voici quelques exemples d'entrelacs brunniens à trois composants qui diffèrent du nœud borroméen.
-
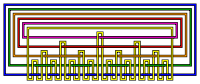
Entrelacs brunnien à 12 croisements.
-
Entrelacs brunnien à 18 croisements.
Liens internes
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Entrelacs brunnien de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Entrelac Brunnien — Entrelacs brunnien Ce nœud à quatre brins est un entrelacs brunnien. En théorie des nœuds, un entrelacs brunnien est un nœud non trivial qui devient trivial si l un quelconque de ses composants est enlevé. En d autres termes, couper n importe… … Wikipédia en Français
Entrelac brunnien — Entrelacs brunnien Ce nœud à quatre brins est un entrelacs brunnien. En théorie des nœuds, un entrelacs brunnien est un nœud non trivial qui devient trivial si l un quelconque de ses composants est enlevé. En d autres termes, couper n importe… … Wikipédia en Français
Hermann Brunn — Pour les articles homonymes, voir Brunn. Hermann Brunn était un mathématicien allemand né en 1862 et mort en 1939. Il est notamment connu pour les entrelacs brunniens, qu il utilise dans un article rédigé en 1892. L appellation entrelacs brunnien … Wikipédia en Français
Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
Liste des articles de mathematiques — Projet:Mathématiques/Liste des articles de mathématiques Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou probabilités et statistiques via l un des trois bandeaux suivants … Wikipédia en Français
Anneaux borroméens — Pour les articles homonymes, voir Borromeo. Nœud borroméen standard. En mathématiques, les anneaux borroméens constituent un entrelacs de trois cercles (au sens … Wikipédia en Français
Noeud Borroméen — Nœud borroméen Nœud borroméen standard. En mathématiques, un nœud borroméen est constitué de trois cercles (au sens topologique) qui sont liés de manière à former un entrelacs brunnien, ce qui signifie qu enlever l un quelconque des trois cercles … Wikipédia en Français
Noeud borromeen — Nœud borroméen Nœud borroméen standard. En mathématiques, un nœud borroméen est constitué de trois cercles (au sens topologique) qui sont liés de manière à former un entrelacs brunnien, ce qui signifie qu enlever l un quelconque des trois cercles … Wikipédia en Français
Noeud borroméen — Nœud borroméen Nœud borroméen standard. En mathématiques, un nœud borroméen est constitué de trois cercles (au sens topologique) qui sont liés de manière à former un entrelacs brunnien, ce qui signifie qu enlever l un quelconque des trois cercles … Wikipédia en Français
Nœud borromeen — Nœud borroméen Nœud borroméen standard. En mathématiques, un nœud borroméen est constitué de trois cercles (au sens topologique) qui sont liés de manière à former un entrelacs brunnien, ce qui signifie qu enlever l un quelconque des trois cercles … Wikipédia en Français