Echelle de temps en mecanique classique

En mécanique classique , le temps est ABSOLU : on l'appelle temps newtonien, t.

Pour résoudre certains problèmes théoriques de mécanique (c'est-à-dire résoudre certaines équations différentielles) , il est parfois astucieux de changer d'échelle de temps , c'est-à-dire , de choisir un nouveau paramètre T =f(t), où t -> f(t) est une fonction croissante de t .

Sommaire 1 Changement affine 2 Changement non affine 3 Méthode de Newton 4 Passage de Hooke à Kepler 5 Echelles de temps et mouvement keplerien 5.1 méthode de Clairaut-Binet 5.2 Méthode de Levi-Civita 6 Voir aussi 6.1 Articles connexes

Changement affine

Dans l'équation du Principe Fondamental de la Dynamique 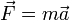, changer t en at+b , ne change que l'origine de la date et l'unité de temps ; ce qui est légitime.

Changement non affine

Ce paragaphe exige de bien manier les dérivées.

Soit T = f(t) et soit t = g(T) la fonction réciproque.

Commencer par examiner ce que cela entraîne au niveau cinématique :

L'intervalle dT au temps t=to vaudra dT = f'(to).dt.

Donc si l'ancienne vitesse était v(t) = d/dt OM , la nouvelle est V(T) =d/dT OM soit réduite du facteur d'échelle f'(to) [égal d'ailleurs à 1/g'(To), bien sûr]:

V(T) = v(t).[dt/dT] = v(t)/f'(t).

mais ce facteur d'échelle varie au cours du temps! Donc, attention à la deuxième dérivation, c'est-à-dire pour l'accélération! En effet :

Si d²f/dt²(t) = 0 , rien de grave n'arrive :

A(T) = (1/f'²). a(t): c'est le changement d'échelle sur l'accélération.

Sinon , A(T) = (1/f'²)[a(t) - f".V].

Donc, avec un "faux-temps" , le PFD s'écrit :

m A(T) = (1/f'²).F + Fcomplémentaire ,

avec Fcomplémentaire = -mV (f"/f'²)!

Méthode de Newton

Newton était bien conscient du fait que changer d'échelle de temps n'était pas anodin! On peut en poursuivant cette analyse retrouver la très célèbre transmutation de la force, de la force de Hooke en la force de gravitation, surtout en tenant compte des formules de l'accélération de Siacci.

Ainsi Newton montra que la MEME trajectoire pouvait être parcourue sous l'action de deux champs centraux différents, certes avec deux mouvements différents:

soit S le premier centre de force. Soit Q le deuxième centre de force, et QM le rayon vecteur. La tangente en M est la même pour les deux mouvements (mais V est différent de v, comme vu précédemment). Soit G le point de cette tangente, intersection avec la demi-droite SG menée de S parallèlement à QM.

Le théorème de Newton est :

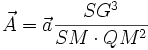
Passage de Hooke à Kepler

Dans le cas d'une ellipse de Hooke (de grand axe 2a), décrite sous l'action d'un champ central issu de O , centre de l'ellipse , et de force -k OM , le théorème précédent conclut : Cette même ellipse peut être décrite par le champ central issu de F avec :

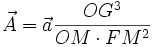
Or , géométriquement, il est facile de prouver que OG = a = cste:

D'où :

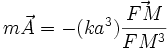
Newton en déduisit que l'ellipse de Kepler pouvait être décrite sous l'action d'une force centrale issue du foyer et en 1/ FM².

On voit ce que peut donner dans des mains expertes la notion de temps-non-absolu! En fait , si Newton a effectivement utilisé la formule précédente, il n'apparaît pas qu'il ait utilisé le changement d'échelle de temps : sa démonstration est directement un tour-de-force géométrique.

Echelles de temps et mouvement keplerien

Néanmoins, en 2006, on a bien compris que le problème mécanique newtonien était "simplement" de résoudre des équations différentielles de la variable t , dit temps absolu. Et depuis 300 ans, les mathématiciens ne se sont pas privés de changer de variable pour résoudre ces équations, le plus aisément possible (cf mouvement keplerien):

méthode de Clairaut-Binet

Voici une échelle de temps particulièrement utile pour le mouvement avec Force centrale: Il s'agit du changement choisi par Clairaut , puis enseigné par Binet à l'École Polytechnique : Comme le champ est central , la deuxième loi de Kepler indique que , si r(t) non nul, l'angle polaire ,theta(t), est fonction monotone croissante de t : on peut donc le choisir comme échelle de temps (cela serait le temps solaire vrai si l'inclinaison de la terre était nulle). Soit :

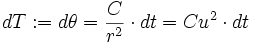• en ayant posé u := 1/r
• un calcul mène à exprimer le vecteur vitesse :

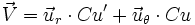
• de même le vecteur accélération :

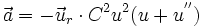
Cela convient "miraculeusement bien" pour la force newtonienne -GM m u² , car on est conduit à une équation d'oscillateur harmonique :

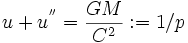
d'où la solution de Kepler u = 1/p + 1/p.e.cos(T-To).

Mais cette méthode ne convient pas si C = 0 (cas du choc).

Méthode de Levi-Civita

On préfère donc parfois choisir une échelle de temps dite régularisante , qui dans le cas de Newton , est appelée échelle de Levi-Civita (bien qu'elle fût connue depuis longtemps. On parle aussi d'échelle KS (Kustaanheimo et Stiefel): dT = dt/r, ce qui évite la divergence des intégrales quand r tend vers zéro.

En fait, pour simplifier, on s'intéresse au cas elliptique; on prendra donc dT = sqrt(-2E)dt/r = Kdt/r(de telle sorte que ce temps T soit adimensionné) : reprenant alors les calculs du cas de changement d'échelle non-affine , on voit qu'il vient : d OM /dT = v r/K ; puis .

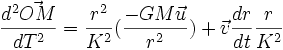Or le vecteur de Runge-Lenz peut s'écrire :

 ;

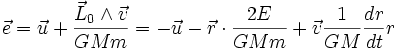ce qui en remplaçant dans l'équation précédente donne :

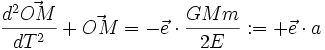
équation d'un oscillateur harmonique, de centre de force excentré !

Bien sûr , tout cela n'est, à ce niveau, que poudre aux yeux puisque l'on a reconnu en T la définition de l'anomalie excentrique et donc que : OM = r = a(1-e cos T) et ωt = T - e sin T.

Mais dans une analyse de symétrie plus soigneuse, il est important de savoir faire ce changement d'échelle.

Voir aussi

Articles connexes

• Temps newtonien
• Mouvement keplerien
• Accélération de Siacci
• Transmutation de la force

• Portail de la physique