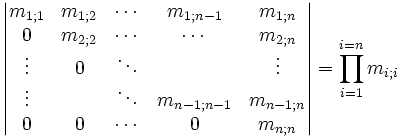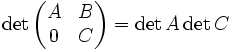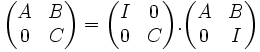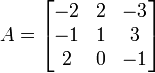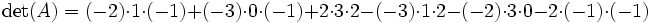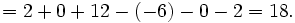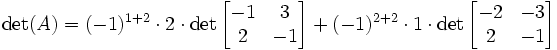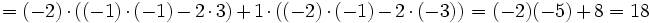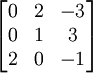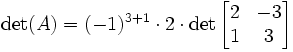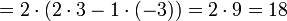Développement d'un déterminant

Développement d'un déterminant

Calcul du déterminant d'une matrice

Il existe de nombreux procédés de calcul du déterminant d'une matrice carrée de taille n à coefficients réels, ou plus généralement à coefficients dans un corps K. La méthode la plus efficace en règle générale est l'utilisation d'une technique de pivot de Gauss.

Sommaire

Cas particuliers simples

  • Les formules des premiers paragraphes s'appliquent dans le cas des dimensions égales à 2 ou à 3.Voir aussi de dimension égales à 4 * Règle de Cramer
  • La règle de Sarrus est un procédé visuel, qui permet de retenir la formule de calcul des déterminants d’ordre 3. Ce n'est toutefois pas toujours la méthode la plus simple ou la plus rapide. Une approche basée sur les propriétés de linéarité du déterminant permet souvent d'effectuer moins d'opérations, ou d'obtenir une forme factorisée plus intéressante.

La règle de Sarrus consiste à écrire les trois colonnes de la matrice et à répéter dans l’ordre, les deux premières lignes en dessous de la matrice. Il suffit alors d’effectuer les produits des coefficients de chaque diagonale et d’en faire la somme si la diagonale est descendante ou la différence si la diagonale est ascendante. Plus clairement : pour calculer \begin{vmatrix}a&b&c\\d&e&f\\g&h&i\end{vmatrix}, il suffit d'effectuer


a b c
d e f
g h i
a b c
d e f
et
a b c
d e f
g h i
a b c
d e f
affectés d'un signe positif affectés d'un signe négatif

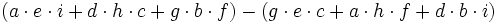et le résultat est (a\cdot e\cdot i + d\cdot h\cdot c + g\cdot b\cdot f) - (g\cdot e\cdot c +a\cdot h\cdot f +d\cdot b\cdot i).

\begin{vmatrix} m_{1;1} & m_{1;2} & \cdots & m_{1;n-1} & m_{1;n} \\ 0 & m_{2;2} & \cdots & \cdots & m_{2;n} \\ \vdots & 0 & \ddots & & \vdots \\ \vdots & & \ddots & m_{n-1;n-1} & m_{n-1;n} \\ 0 & 0 & \cdots & 0 & m_{n;n} \end{vmatrix} = \prod_{i=1}^{i=n}{m_{i;i}}
Démonstration :
On procède par récurrence. Il suffit d'appliquer la formule de Laplace à la première colonne pour se ramener d'une matrice de taille n à une matrice de taille n-1.
\det \begin{pmatrix} A & B \\ 0 & C \end{pmatrix}=\det A \det C
Démonstration
On commence par simplifier la situation en utilisant le produit par blocs suivant
\begin{pmatrix} A & B \\ 0 & C \end{pmatrix}=\begin{pmatrix} I & 0 \\ 0 & C \end{pmatrix}.\begin{pmatrix} A & B \\ 0 & I \end{pmatrix}
Il suffit en effet de prouver que la première matrice a pour déterminant det C, la seconde det A. Mais pour cela on reprend la méthode de démonstration utilisée pour les matrices triangulaires. Ainsi pour la première matrice, on effectue des développements successifs par rapport aux premières lignes, qui sont les plus simples : il ne reste plus que le déterminant de C. Pour la deuxième matrice, on suit une méthode analogue avec les dernières lignes.

Méthodes générales

1. Application directe de la formule de Leibniz

Appliquée en toute généralité, cette formule demande d'effectuer une somme de n! termes, chacun constitué d'un produit de n termes. Sans même prendre en compte le calcul de signature, le nombre de calculs nécessaires dépasse l'ordre (n+1)!.

2. Application récursive de la formule de Laplace

Le calcul d'un déterminant de taille n se ramène à une somme de n déterminants de taille n-1, chacun d'eux étant somme de n-1 déterminants de taille n-2, et ainsi de suite. Le temps de calcul croît de nouveau comme une factorielle en n.
Dans la pratique la formule de Laplace n'est intéressante que si plusieurs des coefficients a(i,j) d'une même colonne (ou d'une même ligne) sont nuls.

3. Utilisation du caractère multilinéaire

On peut suivre une méthode de type pivot de Gauss pour transformer le déterminant par des opérations élémentaires en un déterminant triangulaire dont le calcul est aisé. Le temps de calcul croît alors seulement comme n3.

La dernière méthode est donc celle qu'il convient de privilégier pour un calcul général. Mais si la matrice présente des symétries particulières, une technique adaptée peut permettre de conclure plus aisément.

Exemple

Soit à calculer

A = \begin{bmatrix}-2&2&-3 \\ -1& 1& 3\\ 2 &0 &-1\end{bmatrix}

1. Par utilisation directe de la définition (ou règle de Sarrus, cela revient au même)

\det(A)=(-2)\cdot 1 \cdot (-1) + (-3)\cdot 0 \cdot (-1) + 2\cdot 3\cdot 2 - (-3)\cdot 1 \cdot 2 - (-2)\cdot 3 \cdot 0 - 2\cdot (-1) \cdot (-1)
=2+0+12-(-6)-0-2 = 18.\;

2. Par applications successives de la formule de Laplace (en commençant par la deuxième colonne, la plus avantageuse pour la disposition des zéros)

\det(A)=(-1)^{1+2}\cdot 2 \cdot \det \begin{bmatrix}-1&3\\ 2 &-1\end{bmatrix} + (-1)^{2+2}\cdot 1 \cdot \det \begin{bmatrix}-2&-3\\ 2&-1\end{bmatrix}
=(-2)\cdot((-1)\cdot(-1)-2\cdot3)+1\cdot((-2)\cdot(-1)-2\cdot(-3)) = (-2)(-5)+8 = 18

3. Par utilisation d'une technique de type pivot de Gauss, la première colonne est remplacée par la somme des colonnes 1 et 2

\begin{bmatrix}0&2&-3\\ 0 &1 &3\\ 2 &0 &-1\end{bmatrix}

ce qui rend le développement par rapport à cette colonne évident

\det(A)=(-1)^{3+1}\cdot 2\cdot \det \begin{bmatrix}2&-3\\ 1&3\end{bmatrix}
=2\cdot(2\cdot3-1\cdot(-3)) = 2\cdot 9 = 18

Calculs de déterminants classiques

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Calcul du d%C3%A9terminant d%27une matrice ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Développement d'un déterminant de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Determinant (mathematiques) — Déterminant (mathématiques) Pour les articles homonymes, voir Déterminant. En mathématiques, initialement introduit en algèbre pour déterminer le nombre de solutions d un système d équations linéaires, le déterminant se révèle un outil très… …   Wikipédia en Français

  • Déterminant (Mathématiques) — Pour les articles homonymes, voir Déterminant. En mathématiques, initialement introduit en algèbre pour déterminer le nombre de solutions d un système d équations linéaires, le déterminant se révèle un outil très puissant dans de nombreux… …   Wikipédia en Français

  • DÉVELOPPEMENT ÉCONOMIQUE ET SOCIAL - Économie — Le terme de développement n’est usité dans son acception économique que depuis les années cinquante. Mais l’idée est plus ancienne. Elle constitue le thème central du livre d’Adam Smith, Recherches sur la nature et les causes de la richesse des… …   Encyclopédie Universelle

  • Déterminant (mathématiques) — Pour les articles homonymes, voir Déterminant. En mathématiques, le déterminant fut initialement introduit en algèbre, pour résoudre un système d équations linéaires comportant autant d équations que d inconnues. Il se révèle un outil très… …   Wikipédia en Français

  • Développement de Laplace — Comatrice En algèbre linéaire, la comatrice d une matrice carrée A est une matrice introduite par une généralisation du calcul de l inverse de A. Elle a une importance considérable pour l étude des déterminants. Ses coefficients sont appelés… …   Wikipédia en Français

  • Déterminant par blocs — La formule de déterminant par bloc généralise à la fois les formules de Laplace de calcul du déterminant d une matrice carrée par développement selon une ligne ou une colonne ou le calcul du déterminant d une matrice diagonale ou trigonale par… …   Wikipédia en Français

  • Calcul du déterminant d'une matrice — Le calcul du déterminant d une matrice est un outil nécessaire tant en algèbre linéaire pour vérifier une inversibilité ou calculer l inverse d une matrice qu en analyse vectorielle avec, par exemple, le calcul d un jacobien. S il existe une… …   Wikipédia en Français

  • Facteur déterminant des testicules — Le facteur déterminant des testicules (FDT) est le terme générale désignant le gène (ou son produit) induisant la masculinité chez l Homme et quelques autres espèces. Certains gènes entraînent des réactions chimiques qui induisent le… …   Wikipédia en Français

  • Croissance économique et développement durable — Croissance économique Évolution du PIB par habitant sur les deux derniers millénaires La croissance économique désigne l augmentation de la production de biens et de services dans une économie sur une période donnée[1], qui est généralement une… …   Wikipédia en Français

  • Theorie des vagues de developpement — Théorie des vagues de développement Dans une série d’ouvrages publiés entre 1971 et 1994, dont les plus marquants sont Le Choc du futur, La Troisième vague et Les Nouveaux pouvoirs, Alvin Toffler et son épouse Heidi ont développé une idée fondée… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”