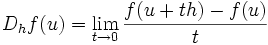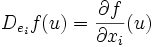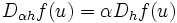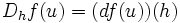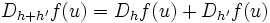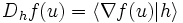Dérivation directionnelle

Dérivation directionnelle

Dérivée directionnelle

En analyse, la dérivée directionnelle est un outil d'analyse à une variable applicable aux fonctions à plusieurs variables. Il permet de décrire les variations infinitésimales d'une fonction dans une direction particulière. On peut définir cette dérivée dans le cadre des espaces vectoriels normés ou des variétés différentielles.

Sommaire

Dérivation pour une fonction définie sur un ouvert d'un espace vectoriel

Soient E un espace vectoriel normé, U un ouvert de E et f fonction définie sur U à valeurs dans un espace vectoriel normé F.

On donnera la qualification de points aux éléments de U et de vecteurs aux éléments de E, les raisons en seront détaillées au-dessous.

Soient donc u un point de U et h un vecteur de E. La dérivée de f au point u dans la direction du vecteur h est définie, lorsque la limite existe, par

D_h f (u)= \lim\limits_{t\to 0} \frac{f(u+th)-f(u)}{t}

Lorsque l'espace E est de dimension finie n et muni d'une base, la fonction f peut être vue comme une fonction de n variables réelles, et le calcul des dérivées directionnelles dans les directions des vecteurs de base est identique au calcul des dérivées partielles de f

D_{e_i} f (u) = \frac{\partial f}{\partial x_i}(u)

Interprétation géométrique

Si h est le vecteur nul, la fonction est automatiquement dérivable de dérivée nulle. On examine les cas pour lesquels h désigne effectivement une direction (h non nul).

La dérivée de la fonction f au point u dans la direction du vecteur h se calcule comme la dérivée en 0 de la fonction d'une seule variable réelle g(t)=f(u+th). Cette dernière s'interprète comme la fonction f lue le long de la droite passant par u et dirigée par h.

Par ailleurs si on remplace h par un vecteur colinéaire αh, le calcul de dérivée est identique à la multiplication par un facteur α près

D_{\alpha h} f(u) = \alpha D_h f(u) \,

En revanche il n'y a pas de raison a priori d'observer un résultat particulier lorsqu'on somme deux vecteurs h et h' .

Cas d'une fonction différentiable

Si la fonction f est différentiable au point u, alors elle admet des dérivées en ce point dans la direction de tout vecteur. Cette dérivée se calcule à partir de l'application différentielle en u (notée df(u)) par application de la formule

D_h f (u)=(df (u))(h)\,

Et cette fois, notamment, on observe que le résultat est linéaire en h. Notamment

D_{h+ h'} f(u) = D_h f(u)+ D_{h'} f(u)\,

Enfin si E est un espace vectoriel de dimension finie n muni d'une base, il est possible de calculer toutes les dérivées directionnelles en termes de dérivées partielles

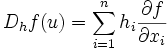D_h f (u)= \sum_{i=1}^n h_i \frac{\partial f}{\partial x_i}.

La réciproque est fausse : le fait qu'une application présente des dérivées en u dans toutes les directions n'assure pas la différentiabilité, ni même la continuité.

Si E est un espace vectoriel euclidien et f une application différentiable à valeurs réelles, il est possible d'utiliser le gradient de f pour exprimer la dérivée directionnelle

D_h f (u)=\langle \nabla f (u)|h \rangle

Ainsi si f présente un extremum local en u le gradient est nul en ce point (pour une étude plus détaillée voir point critique).

Dérivée directionnelle pour les variétés

Définition

Soit f une fonction numérique sur une variété différentielle M. Avec une définition analogue à la précédente, il est loisible d'introduire la dérivée de f en un point m de M et dans la direction d'un vecteur tangent h en m à la variété. Comme la notion de droite dirigée par h n'a plus de sens, il faut la remplacer par une courbe passant par m et de vecteur tangent h en ce point.

Soit γ une courbe tracée sur M, continûment dérivable, vérifiant γ(0)=m et γ'(0)=h. Si la fonction 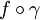f\circ \gamma admet une dérivée en 0, elle est appelée dérivée de f au point m dans la direction de h. On montre en effet que cette définition ne dépend pas de la courbe γ convenable choisie.

Extension : dérivée de Lie

Si X est un champ de vecteurs 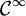{\mathcal C}^\infty sur la variété M et si f est une fonction numérique 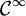{\mathcal C}^\infty sur M, il est possible de calculer les dérivées partielles de f en chaque point p selon le vecteur X(p). La fonction obtenue en considérant toutes ces dérivées est notée 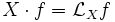X\cdot f = {\mathcal L}_X f et est appelée dérivée de Lie de f par X.

Pour calculer la dérivée de Lie de f, il est notamment possible de prendre pour courbes tangentes aux vecteurs X(p) les courbes intégrales du champ de vecteurs. La généralisation de ce point de vue à la dérivation des champs de vecteurs, formes différentielles et tenseurs est décrit à l'article dérivée de Lie.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « D%C3%A9riv%C3%A9e directionnelle ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Dérivation directionnelle de Wikipédia en français (auteurs)

Игры ⚽ Нужно сделать НИР?

Regardez d'autres dictionnaires:

  • Dérivée directionnelle — En analyse mathématique, la notion de dérivée directionnelle permet de quantifier la variation locale d une fonction dépendant de plusieurs variables, en un point donné et le long d une direction donnée dans l espace de ces variables. Dans la… …   Wikipédia en Français

  • Derivee directionnelle — Dérivée directionnelle En analyse, la dérivée directionnelle est un outil d analyse à une variable applicable aux fonctions à plusieurs variables. Il permet de décrire les variations infinitésimales d une fonction dans une direction particulière …   Wikipédia en Français

  • Dérivée Directionnelle — En analyse, la dérivée directionnelle est un outil d analyse à une variable applicable aux fonctions à plusieurs variables. Il permet de décrire les variations infinitésimales d une fonction dans une direction particulière. On peut définir cette… …   Wikipédia en Français

  • Derivee de Lie — Dérivée de Lie La dérivée de Lie est une opération de différentiation naturelle sur les champs de tenseurs, en particulier les formes différentielles, généralisant la dérivation directionnelle d une fonction sur une variété différentielle. On… …   Wikipédia en Français

  • Dérivée De Lie — La dérivée de Lie est une opération de différentiation naturelle sur les champs de tenseurs, en particulier les formes différentielles, généralisant la dérivation directionnelle d une fonction sur une variété différentielle. On note ici M une… …   Wikipédia en Français

  • Dérivée de Lie — La dérivée de Lie est une opération de différentiation naturelle sur les champs de tenseurs, en particulier les formes différentielles, généralisant la dérivation directionnelle d une fonction sur une variété différentielle. On note ici M une… …   Wikipédia en Français

  • Dérivée de lie — La dérivée de Lie est une opération de différentiation naturelle sur les champs de tenseurs, en particulier les formes différentielles, généralisant la dérivation directionnelle d une fonction sur une variété différentielle. On note ici M une… …   Wikipédia en Français

  • Sous-différentiel — En mathématiques, et plus précisément en analyse convexe, le sous différentiel est un concept permettant de décrire la variation locale d une fonction convexe (à valeurs réelles donc) non nécessairement différentiable dans un sens classique,… …   Wikipédia en Français

  • Fonction B-différentiable — En analyse mathématique, la B différentiabilité est un concept de différentiabiité plus faible que celui de Fréchet, dans lequel l opérateur dérivée n est pas requis d être linéaire et borné, mais seulement positivement homogène et borné. La… …   Wikipédia en Français

  • Méthode des différences finies — En analyse numérique, la méthode des différences finies est une technique courante de recherche de solutions approchées d équations aux dérivées partielles qui consiste à résoudre un système de relations (schéma numérique) liant les valeurs des… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”