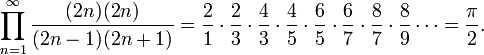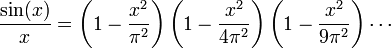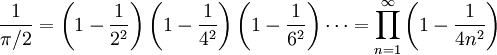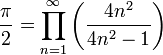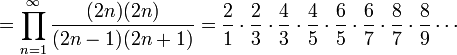Démonstration du produit de Wallis

Démonstration du produit de Wallis

Produit de Wallis

En mathématiques, le produit de Wallis est une expression de la moitié de la constante π sous la forme d'un produit infini, énoncée en 1655 par John Wallis.

Expression

Ce produit peut s'écrire sous la forme :

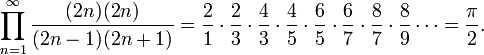
\prod_{n=1}^{\infty} \dfrac{(2n)(2n)}{(2n-1)(2n+1)} = \dfrac{2}{1} \cdot \dfrac{2}{3} \cdot \dfrac{4}{3} \cdot \dfrac{4}{5} \cdot \dfrac{6}{5} \cdot \dfrac{6}{7} \cdot \dfrac{8}{7} \cdot \dfrac{8}{9} \cdots = \dfrac{\pi}{2}.

Démonstration

L'égalité est une conséquence directe de la formule d'Euler-Wallis pour le sinus :

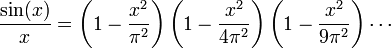
\dfrac{\sin(x)}{x} = \left(1 - \dfrac{x^2}{\pi^2}\right)\left(1 - \dfrac{x^2}{4\pi^2}\right)\left(1 - \dfrac{x^2}{9\pi^2}\right) \cdots

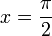Si x=\dfrac{\pi}{2}\,,

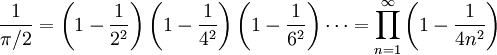
\dfrac{1}{\pi / 2} = \left(1 - \dfrac{1}{2^2}\right)\left(1 - \dfrac{1}{4^2}\right)\left(1 - \dfrac{1}{6^2}\right) \cdots = \prod_{n=1}^{\infty} \left(1 - \dfrac{1}{4n^2}\right)
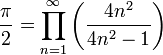
\dfrac{\pi}{2} = \prod_{n=1}^{\infty} \left(\dfrac{4n^2}{4n^2 - 1}\right)
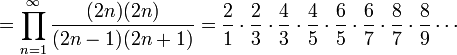
= \prod_{n=1}^{\infty} \dfrac{(2n)(2n)}{(2n-1)(2n+1)} = \dfrac{2}{1} \cdot \dfrac{2}{3} \cdot \dfrac{4}{3} \cdot \dfrac{4}{5} \cdot \dfrac{6}{5} \cdot \dfrac{6}{7} \cdot \dfrac{8}{7} \cdot \dfrac{8}{9} \cdots

Lien externe

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Produit de Wallis ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Démonstration du produit de Wallis de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать курсовую

Regardez d'autres dictionnaires:

  • Produit de wallis — En mathématiques, le produit de Wallis est une expression de la moitié de la constante π sous la forme d un produit infini, énoncée en 1655 par John Wallis. Expression Ce produit peut s écrire sous la forme : Démonstration L égalité est une… …   Wikipédia en Français

  • Produit de Wallis — En mathématiques, le produit de Wallis est une expression de la moitié de la constante π sous la forme d un produit infini, énoncée en 1655 par John Wallis, dans son ouvrage Arithmetica infinitorum. Sommaire 1 Expression 2 Démonstration 3 Vitesse …   Wikipédia en Français

  • John Wallis — Pour les articles homonymes, voir Wallis. John Wallis John Wallis, né le 23 novembre 1616 à Ashford …   Wikipédia en Français

  • John Wallis : Les Applications Cliniques De La Phonétique Et L'éducation Des Sourds — John Wallis Pour les articles homonymes, voir Wallis. John Wallis John Wallis, né le 23 novembre …   Wikipédia en Français

  • John Wallis : les applications cliniques de la phonétique et l'éducation des sourds — John Wallis Pour les articles homonymes, voir Wallis. John Wallis John Wallis, né le 23 novembre …   Wikipédia en Français

  • John wallis : les applications cliniques de la phonétique et l'éducation des sourds — John Wallis Pour les articles homonymes, voir Wallis. John Wallis John Wallis, né le 23 novembre …   Wikipédia en Français

  • Integrales de Wallis — Intégrales de Wallis En analyse, les intégrales de Wallis constituent une famille d intégrales introduites par John Wallis. Sommaire 1 Définition, premières propriétés 2 Relation de récurrence, calcul des intégrales de Wallis …   Wikipédia en Français

  • Intégrale de Wallis — Intégrales de Wallis En analyse, les intégrales de Wallis constituent une famille d intégrales introduites par John Wallis. Sommaire 1 Définition, premières propriétés 2 Relation de récurrence, calcul des intégrales de Wallis …   Wikipédia en Français

  • Intégrales De Wallis — En analyse, les intégrales de Wallis constituent une famille d intégrales introduites par John Wallis. Sommaire 1 Définition, premières propriétés 2 Relation de récurrence, calcul des intégrales de Wallis …   Wikipédia en Français

  • Intégrales de wallis — En analyse, les intégrales de Wallis constituent une famille d intégrales introduites par John Wallis. Sommaire 1 Définition, premières propriétés 2 Relation de récurrence, calcul des intégrales de Wallis …   Wikipédia en Français

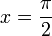Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”