- Droite de Philon
-
Droite de Philon (MN) relative à (Ox) et (Oy) et passant par A
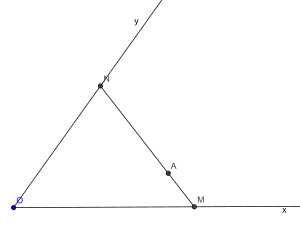
En géométrie plane, la droite de Philon est le plus court segment joignant deux demi-droites données (Ox) et (Oy) et passant par un point A donné[1]. Cette droite porte le nom du mathématicien mécanicien Philon de Byzance qui l'aurait mise en place pour résoudre le problème de la duplication du cube[2].
Sommaire
Propriété caractéristique
Propriété fondamentale — Soit [MN] le segment cherché et H le pied de la hauteur issue de O dans le triangle OMN, [MN] est le segment le plus court si et seulement si les distances AM et HN sont égales;
Démonstration :
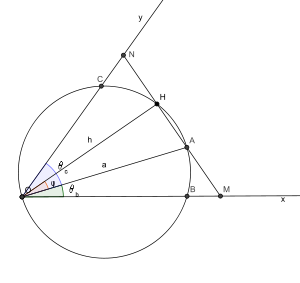
On trace le cercle de diamètre [OA]. Ce cercle rencontre la demi-droite (Ox) en O et B et la demi-droite (Oy) en O et C. Le pied de la hauteur issue de O dans le triangle OMN est le point d'intersection de ce cercle avec la droite (MN). Si on suppose que le point A est plus proche de (Ox) que de (Oy), le plus court chemin MN sera obtenu pour un point H situé sur l'arc de cercle (AC).
On appelle a la distance OA, h la distance OH, φ l'angle AOH, θb l'angle AOB et θc l'angle AOC. La trigonométrie dans les triangles rectangles permet d'obtenir les relations suivantes :
- NH = htan(θc − φ)
- HM = htan(θb + φ)
- HA = htan(φ)
- AM = htan(θb + φ) − htan(φ)
- h = acos(φ)
La distance que l'on cherche à optimiser est alors :
La dérivée de L s'exprime alors sous la forme :
Le signe de la dérivée est donc celui de la différence AM - HN. Lorsque l'angle φ augmente, AM augmente et HN diminue. La différence augmente et passe d'une valeur négative (si H est en A) à une valeur positive (si H est en B) et s'annule donc pour une valeur φ0.
La longueur L(φ) est donc décroissante puis croissante et atteint son minimum pour une valeur φ0 telle que AM=HN
Duplication du cube
Cette construction permet d'insérer deux moyennes proportionnelles entre deux valeurs a et b et en particulier, permet la résolution de la duplication du cube. Philon présente cette méthode dans un ouvrage de mécanique sur la construction d'arme de jet. En effet, il cherchait à doubler la puissance de ses armes et avait conclu que, pour doubler la puissance, il suffisait de doubler le volume de celles-ci[3].
Moyennes proportionnelles
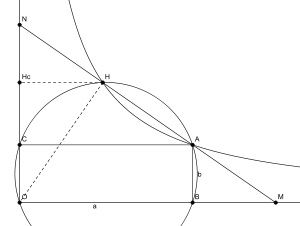
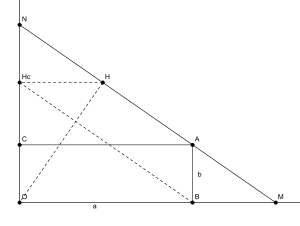
Pour insérer deux moyennes proportionnelles entre les valeurs a et b, il suffit de construire un rectangle OBAC tel que OB=a et BA=b, de construire la droite de Philon pour les demi-droites [OB) et [OC) passant par A. Le point H fournit les deux moyennes proportionnelles. Si Hc est le projeté orthogonal de H sur (OC), on peut glisser deux moyennes proportionnelles entre b et a à l'aide de HHc et OHc.
En effet,
Puisque NH=AM, les triangles NHcH et ABM sont égaux, la droite (HcB) est parallèle à (MN) et l'on peut repérer une série de triangles semblables à NOM : HcOB, HHcO, NHcH d'où l'on tire les égalités de rapports suivantes :
Soit encore :
Cette construction permet en outre de déterminer la racine cubique du rapport a/b et les deux longueurs peuvent être déterminées à l'aide de racines cubiques. Si on note x = HHc et y = HcO, on obtient
En multipliant ces trois rapports entre eux, on en déduit :
Soit encore
Ainsi, on obtient
En particulier, en prenant a=2 et b=1, la valeur x donne la racine cubique de 2.
Construction
Aucune construction à la règle et au compas ne permet de résoudre la duplication du cube, il en est donc de même de la droite de Philon. Mais elle peut être obtenue à l'aide de l'intersection de deux coniques : le point H est en effet situé sur le cercle de diamètre OA, ainsi que sur l'hyperbole d'équation xy=ab
Notes et références
- David Wells, Dictionnaire Penguin des curiosités géométriques, éditions Eyrolles
- Bernard Vitrac, Mécanique et mathématiques à Alexandrie : le cas de Héron, p 22
- Les plus grands scientifiques du bassin méditerranéen, Philon de Byzance
Voir aussi
Liens internes
Liens externes
- (en) Weisstein, Eric W. "Philo Line." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/PhiloLine.html
![t=\sqrt[3]{\frac ab}](5/f45ca9c30029e3f9463d790f20f722a3.png)
![x=\sqrt[3]{ab^2}](f/5bf73730eba909c9ea9640006654b907.png)
![y=\sqrt[3]{a^2b}](a/48a756fc178a1d8854681da81d56026a.png)
Wikimedia Foundation. 2010.
