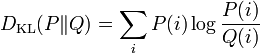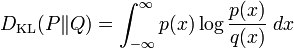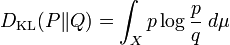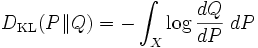Divergence de kullback-leibler

Divergence de Kullback-Leibler

En théorie des probabilités et en théorie de l'information, la divergence de Kullback-Leibler^[1] ^[2] (ou divergence K-L ou encore Entropie relative) est une mesure de dissimilarité entre deux distributions de probabilités P et Q. Elle doit son nom à Solomon Kullback et Richard Leibler, deux cryptanalystes américains ^[3]^[4].

Cette mesure s'interprète comme la différence moyenne du nombre de bits nécessaires au codage d'échantillons de P selon que le codage est choisi optimal pour la distribution P ou Q. Typiquement, P représente les données, les observations, ou une distribution de probabilités calculée avec précision. La distribution Q représente typiquement une théorie, un modèle, une description ou une approximation de P.

La divergence de Kullback-Leiber entre dans la catégorie plus large des f-divergences, introduite indépendamment par Csiszár^[5] en 1967 et par Ali et Silvey ^[6] en 1966. Bien que souvent considérée comme une distance, elle n'en remplit pas tous les axiomes : elle n'est pas symétrique et ne respecte pas l'inégalité triangulaire.

Définition

Pour deux distributions de probabilités discrètes P et Q la divergence de Kullback–Leiber de Q par rapport à P est définie par

$D_{\mathrm{KL}}(P\|Q) = \sum_i P(i) \log \frac{P(i)}{Q(i)} \!$

Pour des distributions P et Q continues on utilise une intégrale

$D_{\mathrm{KL}}(P\|Q) = \int_{-\infty}^{\infty} p(x) \log \frac{p(x)}{q(x)} \; dx \!$

où p et q sont les densités respectives de P et Q.

On peut généraliser les deux cas particuliers ci-dessus en considérant P et Q deux mesures définies sur un ensemble X, absolument continues par rapport à une mesure $μ$ : le Théorème de Radon-Nikodym-Lebesgue assure l'existence des densités p et q avec $d P = p d μ$ et $d Q = q d μ$ , on pose alors

$D_{\mathrm{KL}}(P\|Q) = \int_X p \log \frac{p}{q} \;d\mu \!$

sous réserve que la quantité de droite existe. Si P est absolument continue par rapport à Q, (ce qui est nécessaire si 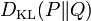$D_{\mathrm{KL}}(P\|Q)$ est finie) alors 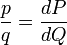$\frac{p}{q} = \frac{dP}{dQ}$ est la dérivée de Radon-Nikodym de P par rapport à Q et on obtient

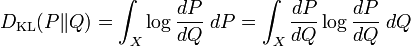$D_{\mathrm{KL}}(P\|Q) = \int_X \log \frac{dP}{dQ} \; dP = \int_X \frac{dP}{dQ} \log\frac{dP}{dQ}\; dQ$ ,

où l'on reconnait l'entropie de P par rapport à Q.

De même, si Q est absolument continue par rapport à P, on a

$D_{\mathrm{KL}}(P\|Q) = -\int_X \log \frac{d Q}{d P} \; dP \!$

Dans les deux cas, on constate que la divergence de Kullback-Leibler ne dépend pas de la mesure $μ$

Lorsque les logarithmes de ces formules sont pris en base 2 l'information est mesurée en bits; lorsque la base est e, l'unité est le nats.

Références

↑ S. Kullback and R. Leiber, « On information and sufficiency », dans Annals of Mathematical Statistics, vol. 22, 1951, p. 79-86
↑ (en) S. Kullback, Information theory and statistics, John Wiley and Sons, NY, 1959
↑ Dr. Solomon Kullback sur www.nsa.gov
↑ Dr. Richard Leiber sur www.nsa.gov
↑ I. Csiszár, « Information-type measures of difference of probability distributions and indirect observation », dans Studia Sci. Math. Hungar., vol. 2, 1967, p. pp. 229-318
↑ M. S. Ali and D. Silvey, « A general class of coefficients of divergence of one distribution from another », dans Journal of the Royal Statistical Society, Ser. B, vol. 28, 1967, p. 131-140

Portail des mathématiques

Ce document provient de « Divergence de Kullback-Leibler ».

Catégories : Probabilités | Théorie de l'information

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Divergence de kullback-leibler de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

Divergence De Kullback-Leibler — En théorie des probabilités et en théorie de l information, la divergence de Kullback Leibler[1] [2] (ou divergence K L ou encore Entropie relative) est une mesure de dissimilarité entre deux distributions de probabilités P et Q. Elle doit son… … Wikipédia en Français
Divergence de Kullback-Leibler — En théorie des probabilités et en théorie de l information, la divergence de Kullback Leibler[1], [2] (ou divergence K L ou encore entropie relative) est une mesure de dissimilarité entre deux distributions de probabilités P et Q. Elle doit son… … Wikipédia en Français
Kullback–Leibler divergence — In probability theory and information theory, the Kullback–Leibler divergence[1][2][3] (also information divergence, information gain, relative entropy, or KLIC) is a non symmetric measure of the difference between two probability distributions P … Wikipedia
Divergence (disambiguation) — Divergence can refer to: In mathematics: Divergence, a function that associates a scalar with every point of a vector field Divergence (computer science), a computation which does not terminate (or terminates in an exceptional state) Divergence… … Wikipedia
Divergence (statistics) — In statistics and information geometry, divergence or a contrast function is a function which establishes the “distance” of one probability distribution to the other on a statistical manifold. The divergence is a weaker notion than that of the… … Wikipedia
Jensen–Shannon divergence — In probability theory and statistics, the Jensen Shannon divergence is a popular method of measuring the similarity between two probability distributions. It is also known as information radius (IRad) [cite book |author=Hinrich Schütze;… … Wikipedia
Solomon Kullback — Dr Solomon Kullback (b. Birth date|1907|04|03 d. Death date|1994|08|05) was a US cryptanalyst and mathematician.Kullback was one of the first three employees hired by William F. Friedman at the US Army s Signal Intelligence Service (SIS) in the… … Wikipedia
Richard Leibler — (March 18, 1914–October 25, 2003) was an American mathematician and cryptanalyst. While working at the NSA, he and Solomon Kullback formulated the Kullback Leibler divergence, a measure of similarity between probability distributions which has… … Wikipedia
Bregman divergence — In mathematics Bregman divergence or Bregman distance is similar to a metric, but does not satisfy the triangle inequality nor symmetry. There are two ways in which Bregman divergences are important. Firstly, they generalize squared Euclidean… … Wikipedia
Entropie relative — Divergence de Kullback Leibler En théorie des probabilités et en théorie de l information, la divergence de Kullback Leibler[1] [2] (ou divergence K L ou encore Entropie relative) est une mesure de dissimilarité entre deux distributions de… … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Divergence de kullback-leibler