- Distance de levenshtein
-
Distance de Levenshtein
La distance de Levenshtein mesure la similarité entre deux chaînes de caractères. Elle est égale au nombre minimal de caractères qu'il faut supprimer, insérer ou remplacer pour passer d’une chaîne à l’autre.
Son nom provient de Vladimir Levenshtein qui l'a définie en 1965. Elle est aussi connue sous le nom de « distance d'édition » ou encore de « déformation dynamique temporelle », notamment en reconnaissance vocale.
Cette distance est d'autant plus grande que le nombre de différences entre les deux chaînes est grand. La distance de Levenshtein peut être considérée comme une généralisation de la distance de Hamming. On peut montrer en particulier que la distance de Hamming est un majorant de la distance de Levenshtein.
Sommaire
Définition
On appelle distance de Levenshtein entre deux mots M et P le coût minimal pour aller de M à P en effectuant les opérations élémentaires suivantes:
- substitution d'un caractère de M en un caractère de P.
- ajout dans M d'un caractère de P.
- suppression d'un caractère de M.
On associe ainsi à chacune de ces opérations un coût. Par exemple, dans les exemples suivants, le coût est toujours égal à 1, sauf dans le cas d'une substitution de caractères identiques.
Exemples
Si M = « examen » et P = « examen », alors LD (M, P) = 0, parce qu'aucune opération n'a été réalisée.
Si M = « examen » et P = « examan », alors LD (M, P) = 1, parce qu’il y a eu un remplacement (changement du e en a).
Algorithme de Levenshtein
L'algorithme ci-dessous permet de calculer la distance de Levenshtein entre deux chaînes de caractères courtes. Pour des chaînes de caractères plus longues (plusieurs mots), il faut utiliser les algorithmes de Jaccard ou TF/IDF par exemple. L'algorithme de Levenshtein est un algorithme de programmation dynamique (solution de type du bas en haut), qui utilise une matrice de dimension
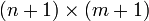où n et m sont les dimensions des deux chaînes de caractères. Dans le pseudo-code suivant, la chaîne chaine1 est de longueur longueurChaine1 et chaine2, de longueur longueurChaine2. Cet algorithme renvoie un entier positif ou nul. Il renvoie 0 si les chaînes 1 et 2 sont égales. Si les chaînes 1 et 2 sont très différentes, la fonction renverra au maximum la plus grande longueur des deux chaînes.entier DistanceDeLevenshtein(caractere chaine1[1..longueurChaine1], caractere chaine2[1..longueurChaine2]) // d est un tableau de longueurChaine1+1 rangées et longueurChaine2+1 colonnes declarer entier d[0..longueurChaine1, 0..longueurChaine2] // i et j itèrent sur chaine1 et chaine2 declarer entier i, j, coût pour i de 0 à longueurChaine1 d[i, 0] := i pour j de 0 à longueurChaine2 d[0, j] := j pour i de 1 à longueurChaine1 pour j de 1 à longueurChaine2 si chaine1[i] = chaine2[j] alors coût := 0 sinon coût := 1 d[i, j] := minimum( d[i-1, j ] + 1, // effacement d[i, j-1] + 1, // insertion d[i-1, j-1] + coût // substitution ) retourner d[longueurChaine1, longueurChaine2]L'invariant est qu'on peut transformer le segment initial
chaine1[1..i]enchaine2[1..j]en utilisant un nombre minimal ded[i, j]opérations. L'algorithme achevé, la solution est contenue dans la dernière position à droite de la rangée du bas de la matrice.Améliorations possibles
L'algorithme présenté a une complexité temporelle et spatiale de
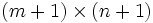. En effet, il faut stocker et remplir la matrice en mémoire. Cependant, il est possible d'effectuer le calcul en ne gardant que la ligne précédente et la ligne actuelle en mémoire, ce qui réduit grandement la quantité de mémoire utilisée à O(m).D'autre part, il est aussi possible d'expliciter les suites d'opérations permettant de réellement passer d'une chaîne à l'autre. Une fois le calcul effectué, on peut obtenir ces suites en partant de la cellule en bas à droite et en remontant de cellule en cellule en prenant à chaque fois la ou les cellules à l'origine de la valeur minimum. Plusieurs cellules pouvant être à l'origine de cette valeur minimum, aussi plusieurs chemins peuvent être déduits, ils sont tous de longueur minimum. Ce processus permet par exemple d'apparier les caractères de a avec ceux de b.
Des implémentations plus complexes mais plus performantes existent[1] par exemple celle de Myers[2] dont le coût est en O(ND) avec D la distance et surtout celle de Wu, Manber et Myers[3] en O(NP) ou P=D/2 − (N −M)/2.
Implémentations
Plusieurs implémentations sont disponibles : Levenshtein distance.
Exemple de déroulement de l'algorithme
Pour comprendre le fonctionnement de cet algorithme, prenons un exemple:
Soit s= « NICHE » Soit t= « CHIENS »
Intuitivement
Intuitivement, on voit bien que l'on peut transformer la chaîne s en t en 5 étapes:
- Suppression de N et I
- Ajout de I, N et S → CHIENS
La distance de Levenshtein d entre "NICHE" et "CHIENS" est donc d'au plus 5. On peut se convaincre par l'expérience que 5 est effectivement la distance entre les deux chaînes (l'algorithme de la distance de Levenshtein ne s'occupe pas de déplacement, il ne sait détecter que la suppression ou l'insertion d'une lettre, ainsi que le remplacement d'une lettre par une autre). Pour le vérifier formellement, on peut appliquer l'algorithme (ou tout essayer manuellement).
Fonctionnement
Soit n la longueur de la chaîne s (ici n=5)
Soit m la longueur de la chaîne t (ici m=6)Si n=0 alors retourner d=m et quitter
Si m=0 alors retourner d=n et quitterConstruire une matrice M de n+1 lignes et m+1 colonnes.
Initialiser la première ligne par la matrice ligne [ 0,1,….., m-1, m] et la première colonne par la matrice colonne [ 0,1,….., n-1, n]C H I E N S 0 1 2 3 4 5 6 N 1 0 0 0 0 0 0 I 2 0 0 0 0 0 0 C 3 0 0 0 0 0 0 H 4 0 0 0 0 0 0 E 5 0 0 0 0 0 0 Soit Cout(i, j)=0 si A(i)=B(j) et Cout(i, j)=1 si A(i)!=B(j)
On a donc ici la matrice Cout:C H I E N S N 1 1 1 1 0 1 I 1 1 0 1 1 1 C 0 1 1 1 1 1 H 1 0 1 1 1 1 E 1 1 1 0 1 1 On remplit ensuite la matrice M en utilisant la règle suivante M[i, j] est égale au minimum de:
- L’élément directement avant plus 1: M[i-1, j] + 1. (insertion)
- L’élément directement au-dessus plus 1: M[i, j-1] + 1. (effacement)
- Le diagonal précédent plus le coût: M[i-1, j-1] + Cout(i-1, j-1). (substitution)
Attention ! Il s'agit de Cout(i-1, j-1) et non de Cout(i, j) car la matrice Cout est moins grande que la matrice M, ce qui entraîne un décalage.
Dans notre cas, le remplissage de la première ligne donne alors:
C H I E N S 0 1 2 3 4 5 6 N 1 1 2 3 4 4 5 I 2 0 0 0 0 0 0 C 3 0 0 0 0 0 0 H 4 0 0 0 0 0 0 E 5 0 0 0 0 0 0 Nous réitérons cette opération jusqu'à remplir la matrice :
C H I E N S 0 1 2 3 4 5 6 N 1 1 2 3 4 4 5 I 2 2 2 2 3 4 5 C 3 2 3 3 3 4 5 H 4 3 2 3 4 4 5 E 5 4 3 3 3 4 5 La distance de Levenshtein entre les mots s et t se retrouve en M[n, m].
Ici, on retrouve bien les 5 opérations trouvées de manière intuitive, la dernière matrice fournit aussi explicitement une des suites d'opérations permettant de passer d'une chaîne de caractères à l'autre (Il existe 3 suites possibles).
Généralisation
En remplaçant chaîne de caractères par séquence de symboles, les symboles étant comparables par un opérateur d'égalité, on peut définir une distance d'édition fonctionnant sur d'autres types que des chaînes de caractères.
Notes
- ↑ Implémentation en O(NP) sous Delphi Angus Johnson
- ↑ An O(ND) Difference Algorithm and its Variations E Myers - Algorithmica Vol. 1 No. 2, 1986, pp. 251-266
- ↑ An O(NP) Sequence Comparison Algorithm Sun Wu, Udi Manber & Gene Myers
Articles connexes
- Distance de Damerau-Levenshtein
- Distance de Hamming
- Distance d'édition sur les arbres
- diff
- Implémentation en plusieurs langages de programmation
- Jaro
- Distance de Jaro-Winkler
- Indice et distance de Jaccard
- TF-IDF
- Sam Chapman
- William W. Cohen
Portail de l’informatique
Catégories : Algorithme sur les chaînes de caractères | Théorie des codes
Wikimedia Foundation. 2010.
