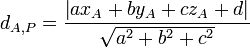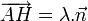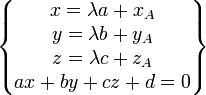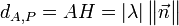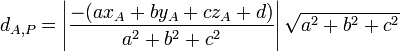Distance d'un point a un plan dans l'espace cartesien

Distance d'un point a un plan dans l'espace cartesien

Distance d'un point à un plan

Dans l'espace euclidien, la distance d'un point à un plan est la plus courte distance séparant ce point et un point du plan. Le théorème de Pythagore permet d'affirmer que la distance du point A au plan (P) correspond à la distance séparant A de son projeté orthogonal H sur le plan (P).

Si l'espace est muni d'un repère orthonormal, les points peuvent être définis à l'aide de leurs coordonnées dites cartésiennes.

Soit le plan P et le point A dans l'espace. On appelle (xA,yA,zA) les coordonnées du point A et ax + by + cz + d = 0 l'équation représentative du plan P : alors la distance du point A au plan P, dA,P vaut :

d_{A,P} =\frac{\left| ax_A + by_A + cz_A + d \right|}{\sqrt{a^2 + b^2 + c^2}}

Démonstration :

Soit H: = (x,y,z) le projeté orthogonal de A sur P et soit 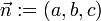\vec n:=(a, b,c) un vecteur normal à P.

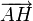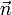On sait que les vecteurs \overrightarrow{AH} et \vec n sont colinéaires, on peut donc écrire  :

\overrightarrow{AH}=\lambda.\vec n

Soit encore

(x − xA;y − yA;z − zA) = λ(a;b;c)

et 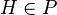H \in P donc

ax + by + cz + d = 0

Ceci revient à résoudre le système suivant:

\begin{Bmatrix} x=\lambda a+x_A \\ y=\lambda b+y_A \\ z=\lambda c+z_A \\ ax+by+cz+d=0 \end{Bmatrix}

La substitution de x, y et z dans la 4e équation par leurs valeurs obtenues dans les 3 premières permet d'écrire:

a(λa + xA) + b(λb + yA) + c(λc + zA) + d = 0.

Ou encore:

axA + byA + czA + d + λ(a2 + b2 + c2) = 0.

P étant un plan, a, b, c ne sont pas tous nuls: on a

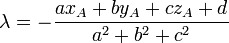
\lambda = - \frac {ax_A+by_A+cz_A+d}{a^2+b^2+c^2}

Or, la distance de A à P, n'est autre que la longueur du vecteur \overrightarrow{AH}; donc:

d_{A,P} =AH=\left| \lambda \right| \begin{Vmatrix} \vec n \end{Vmatrix}
d_{A,P} = \left| \frac {-(ax_A+by_A+cz_A+d)}{a^2+b^2+c^2} \right| \sqrt{a^2+b^2+c^2}
d_{A,P} =\frac{\left| ax_A + by_A + cz_A + d \right|}{\sqrt{a^2 + b^2 + c^2}}

Ceci termine la preuve.

Voir aussi

  • Portail de la géométrie Portail de la géométrie
Ce document provient de « Distance d%27un point %C3%A0 un plan ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Distance d'un point a un plan dans l'espace cartesien de Wikipédia en français (auteurs)

Игры ⚽ Поможем сделать НИР

Regardez d'autres dictionnaires:

  • Distance D'un Point À Un Plan Dans L'espace Cartésien — Distance d un point à un plan Dans l espace euclidien, la distance d un point à un plan est la plus courte distance séparant ce point et un point du plan. Le théorème de Pythagore permet d affirmer que la distance du point A au plan (P)… …   Wikipédia en Français

  • Distance d'un point à un plan dans l'espace cartésien — Distance d un point à un plan Dans l espace euclidien, la distance d un point à un plan est la plus courte distance séparant ce point et un point du plan. Le théorème de Pythagore permet d affirmer que la distance du point A au plan (P)… …   Wikipédia en Français

  • Distance (Mathématiques) — Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. Sommaire 1 Distance sur un ensemble …   Wikipédia en Français

  • Distance (mathematiques) — Distance (mathématiques) Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. Sommaire 1 Distance sur un… …   Wikipédia en Français

  • Distance euclidienne — Distance (mathématiques) Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. Sommaire 1 Distance sur un… …   Wikipédia en Français

  • Distance (mathématiques) — Pour les articles homonymes, voir Distance. En mathématiques, une distance est une application qui formalise l idée intuitive de distance, c est à dire la longueur qui sépare deux points. C est par l analyse des principales propriétés de la… …   Wikipédia en Français

  • point — 1. point [ pwɛ̃ ] n. m. • 1175 « endroit, moment »; lat. punctum « piqûre », de pungere → poindre I ♦ A ♦ Portion de l espace déterminée avec précision. 1 ♦ Endroit, lieu. En divers, en plusieurs points. « il relevait la tête et fixait son regard …   Encyclopédie Universelle

  • Espace Euclidien — En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique classique, le… …   Wikipédia en Français

  • Espace euclidien (algèbre linéaire) — Espace euclidien En mathématiques, un espace euclidien est un objet algébrique permettant de généraliser de façon naturelle la géométrie traditionnelle développée par Euclide, dans ses Éléments. Une géométrie de cette nature modélise, en physique …   Wikipédia en Français

  • ESPACE-TEMPS — La mécanique classique, sous la forme mathématique rigoureuse que lui a donnée Newton, repose sur les deux concepts fondamentaux d’espace et de temps absolus: un événement ponctuel est parfaitement déterminé lorsqu’on connaît sa position dans… …   Encyclopédie Universelle

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”