Detection de collision

Dans les simulations physiques, les jeux vidéos et la géométrie algorithmique, la détection de collision implique l'utilisation d'algorithmes pour tester les collisions (intersection de solides donnés), pour calculer des trajectoires, les dates d'impact et des points d'impact dans une simulation physique.

Sommaire 1 Vue d'ensemble 2 Détection de collision dans une simulation physique 2.1 En d'autres mots 2.2 A posteriori ou a priori 3 Optimisation 3.1 n-body pruning 3.2 Exploiter la cohérence temporelle 3.3  Pairwise pruning  ⇔  Élagage par paires 3.4 Détection de collision par pair exactes 3.5 A priori de taillage 3.6 Partitionnement spatiale, divers 4 Jeux vidéo 5 Références et notes 6 Voir aussi

Vue d'ensemble

Dans la simulation physique, on souhaite procéder à des expériences, comme jouer au billard. La physique des billes de billard est bien décrite, à l'aide de modèles de mouvement de corps rigide et de collision élastique. Une description initiale de la scène devrait être donnée, avec un description physique précise de la table de billard et des billes, de même que les positions initiales de toutes les billes. Étant donné une certaine impulsion initiale sur la bille blanche (résultant probablement d'un joueur tapant la bille à l'aide de sa queue), nous voulons calculer les trajectoires, les déplacements précis et les positions finales de toutes les billes avec un programme informatique. Un programme pour simuler ce jeu possèderait plusieurs parties, l'une d'elles serait responsable du calcul des impacts précis entre les billes de billard. Cet exemple en particulier se révèle est très sensible aux instabilités numériques : une petite erreur dans un calcul pourrait causer des changements importants dans les positions finales des billes.

Les jeux vidéos ont des besoins similaires, avec quelques différences cruciales. Alors que la simulation physique doit simuler la physique du monde réel aussi précisément que possible, les jeux vidéos peuvent le faire d'une manière seulement acceptable, en temps réel et de manière robuste. Les compromis sont autorisés, tant que la simulation résultante est satisfaisante pour le joueur.

En géométrie algorithmique, on s'intéresse aux algorithmes permettant d'obtenir une détection précise des collisions (plus comme les simulateurs physiques). Cependant, il faut que ces algorithmes aient de bons temps d'exécution. Malheureusement, la plupart des algorithmes utilisés dans les simulations physiques et les jeux vidéos n'ont pas une complexité satisfaisante dans le pire des cas, du point de vue de la notation de Landau, même s'il s'avère qu'en pratique ils fonctionnent très bien.

Détection de collision dans une simulation physique

Les simulateurs physiques diffèrent dans la manière dont ils réagissent à une collision. Il y a un gouffre énorme entre une approche KISS et une approche maligne. Certains utilisent la dureté de la matière pour calculer une force, ce qui résoudra la collision dans les étapes qui suivent d'une manière proche de la réalité. Ce calcul peut être très consommateur de CPU, selon la mollesse de l'objet. Certains simulateurs estiment la date de la collision via une interpolation linéaire, reviennent en arrière dans la simulation, et calculent la collision à l'aide de la méthode la plus abstraite des lois de conservation.

Certains itèrent sur l'interpolation linéaire (méthode de Newton) pour calculer la date de la collision avec une plus grande précision que le reste de la simulation. La détection de collisions utilise la cohérence du temps pour permettre des étapes de temps plus fines sans augmenter la charge du CPU (voir par exemple le Contrôle du trafic aérien).

Après une collision rigide, des états particuliers de glissement et d'immobilité peuvent apparaître. Par exemple, l'Open Dynamics Engine utilise des contraintes pour les simuler. Les contraintes évitent l'inertie, et par conséquent l'instabilité. L'implémentation de l'immobilité par un graphe de scène évite d'avoir des objets qui dérivent.

En d'autres mots

Les simulateurs physiques fonctionnement généralement de deux manières : a posteriori ou a priori. En plus de cette distinction, la plupart des algorithmes modernes de détection de collision sont divisés en une hiérarchie d'algorithmes.

A posteriori ou a priori

Dans le cas a posteriori, on fait progresser la simulation physique pendant un petit intervalle de temps, puis on vérifie si des objets se rencontrent. À chaque étape de la simulation, une liste de tous les corps en collision est crée, et les positions et trajectoires de ces objets sont corrigées pour prendre en compte la collision. Nous disons que cette méthode est a posteriori parce qu'on manque typiquement le moment réel de la collision ; on ne la détecte que lorsqu'elle a effectivement eu lieu.

Dans les méthodes a priori, on écrit un algorithme de détection de collisions qui sera capable de prédire très précisément les trajectoires des corps physiques. Les instants des collisions sont calculés avec une grande précision, et les corps physiques ne se coupent jamais. On appelle cela a priori car on calcule les instants des collision avant de mettre à jour la configuration des objets.

Les principaux avantages des méthodes a posteriori sont que, dans ce cas, l'algorithme de détection de collision n'a pas besoin de considérer une innombrable quantité de variables physiques ; une simple liste des objets est donnée à l'algorithme et le programme retourne une liste d'objets en collision. L'algorithme de détection de collision n'a pas besoin de gérer la friction, les collisions élastiques, ou pire, les collisions non élastiques et les corps déformables. De plus, les algorithmes a posteriori sont en pratique d'une dimension plus simple que les algorithmes a priori. En effet, un algorithme a priori doit gérer une variable de temps, qui est absente du problème a posteriori.

D'un autre coté, les algorithmes a posteriori posent des problèmes à l'étape de correction, où les intersections (qui ne sont pas physiquement correctes) doivent être corrigées. En fait, un tel algorithme est parfois considéré comme intrinsèquement imparfait et instable.

Les avantages des algorithmes a priori augmentent la fidélité et la stabilité. Il est difficile (mais pas complètement impossible) de séparer la simulation physique de l'algorithme de détection de collision. Cependant, dans les cas non simples, le problème de déterminer en avance la date de collision de deux objets (étant donné quelques données initiales) n'a pas de solution bien définie -- un algorithme de recherche d'un zéro d'une fonction est en général nécessaire.

Étant donné qu'il est impossible d'obtenir les valeurs exactes, on peut aussi utiliser un simple algorithme a posteriori puis utiliser une recherche dichotomique pour tenter de calculer le moment initial d'une collision, s'il y en a. Cependant, en dehors du fait que cette méthode peut rater certaines collisions, la recherche dichotomique est connue pour être relativement inefficace comparée à d'autres méthodes de recherche de zéro, telle que la méthode de Newton.

Certains objets restent en contact, c'est à dire en collision mais sans rebondir ni s'interpénétrer, tel un vase posé sur une table. Dans tous les cas, la situation de contact requiert un traitement spécial: si deux objets sont en collision (a posteriori) ou glissent (a priori) et que le leur mouvement relatif est en dessous d'un seuil, le frottement devient adhérence et les deux objets sont arrangés dans le même graphe de scène. Cependant, cela pourrait poser des problèmes dans les algorithmes a posteriori^{[réf. nécessaire]}.

Optimisation

Les approches naïves de détection de collision parmi plusieurs objets sont très lentes. Tester chaque objet avec chaque autre fonctionnera mais est trop inefficace pour être utilisé quand le nombre d'objets est grand. Appliqué à des objets à la géométrie complexe, en testant chaque face avec chaque face de l'autre objet est en soit assez lent. Par conséquent, des recherches considérables ont été effectuées pour accélérer la résolution de ce problème.

n-body pruning

 n-body pruning  ⇔  Élagage à n corps Pour les problèmes où plusieurs corps bougent simultanément (comme des boules de billard) une étape de pré-sélection permet de réduire le nombre de paires d'objets que l'on doit considérer dans la collision.

Avec n objets, il y a 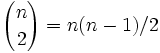paires d'objets qui peuvent éventuellement entrer en collision (voir Coefficient binomial). Itérer parmi toutes les paires donnerait un algorithme avec une complexité temporelle en O(n²). Dans l'exemple du billard, avec treize billes sur la table, soixante-dix-huit paires seront testées. Cependant, s'il n'y a que sept billes dans la moitié nord de la table et six dans la partie sud, alors on peut se limiter à tester les billes de la partie nord entre elles, de même pour celle de la partie sud. Dans ce cas, seulement trente-six paires de billes seront testées.

Le problème est que pour de gros objets très proches les uns des autres, il n'est pas toujours facile de trouver une droite (comme dans l'exemple du billard) qui sépare les objets en deux ensembles sans intersection. Cela peut être corrigé à l'aide d'un algorithme être récursif ; on obtient alors un programme qui semble fonctionner plus rapidement que l'approche naïve en général.

Du point de vue du comportement dans le pire des cas, on remarque que si tous les n objets occupent le même point de l'espace, alors il faudra tester n(n − 1) / 2 = O(n²) paires. C'est pour cela qu'on s'intéresse plutôt à des algorithmes dont la complexité temporelle s'exprime en fonction de la taille de leur sortie. Dans notre cas, ces algorithmes s'exécuteront plus rapidement si le nombre de collisions est petit.

Exploiter la cohérence temporelle

Dans beaucoup d'applications, la disposition des corps physiques change très peu d'une étape de temps à une autre. Certains objets ne bougent même pas. Des algorithmes ont été créés pour que les calculs fait dans une étape précédente puissent être réutilisé à l'étape courante.

D'un point de vue macroscopique, l'objectif de la détection de collision est de trouver des paires d'objets qui peuvent éventuellement se croiser. Ces paires nécessiteront un traitement ultérieur. Un algorithme performant pour effectuer cela a été développé par M. C. Lin de l'université de Berkley [1], qui suggéra d'utiliser des boîtes englobantes pour tous les objets de la scène.

En trois dimensions, chaque boîte est représentée par le produit cartésien de trois intervalles (une boîte serait ). On observe que deux boîtes 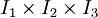et 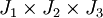se croisent si et seulement si I₁ croise J₁, I₂ croise J₂ et I₃ croise J₃. On suppose que d'une étape de temps à la suivante, si I_k et J_k se croisent, alors il est fort probable qu'ils soient toujours croisés à l'étape suivante. De même, s'ils ne se croisent pas à l'étape précédente, il est fort probable qu'ils ne se croisent toujours pas à l'étape suivante.

Ainsi nous réduisons le problème à celui de suivre, d'une étape à l'autre, quels intervalles se croisent. Nous avons une liste d'intervalles (une pour chaque axe), toutes de même longueur (égale au nombre n de boîtes englobantes). Dans chaque liste, chaque intervalle peut croiser tous les autres. Donc, pour chaque liste, nous avons une matrice M = (m_ij) de valeurs binaires et de de taille 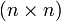 : m_ij = 1 si les intervalles i et j se croisent.

Par hypothèse, la matrice M associée à une liste d'intervalles sera quasiment inchangée d'une étape à une autre. Pour exploiter cela, la liste d'intervalles est implémentée avec une liste des bornes d'intervalle. À chaque élément de la liste est associé les coordonnées des bornes de fin d'intervalle, ainsi qu'un identifiant entier unique représentant cet intervalle. Puis, un algorithme de tri est appliqué pour trier la liste par coordonnée et mettre à jour la matrice M dans la foulée. Il n'est pas difficile de voir que cet algorithme sera relativement rapide si, en effet, la disposition des boîtes ne change pas significativement d'une étape à l'autre.

Dans le cas de corps déformables, tels que des vêtements, il se peut qu'un tel algorithme ne soit pas applicable et qu'un algorithme n-body pruning soit le meilleur.

Si la vitesse des objets est bornée supérieurement, alors les paires d'objets peuvent être filtrées selon la distance les séparant et la durée d'une étape de temps.

 Pairwise pruning  ⇔  Élagage par paires

Une fois que nous avons choisi une paire de corps physiques pour davantage de recherches, nous devons vérifier les collisions plus soigneusement. Cependant, dans beaucoup d'applications, différents objets (s'ils ne sont pas trop déformables) sont décrits par un ensemble de plus petites primitives, principalement des triangles. Aussi maintenant, nous avons deux ensembles de triangles, S = S₁,S₂,...,S_n et T = T₁,T₂,...,T_n (pour simplifier, nous supposerons que chaque ensemble a le même nombre de triangles).

La chose évidente à faire est d'examiner tous les triangles S_j face à tout les triangles T_k pour les collisions, mais ceci implique des comparaisons de n², lesquelles sont déplaisantes. Si possible, il est souhaitable d'employer un algorithme de taille pour réduire le nombre de paires de triangles que nous devons vérifier.

La famille la plus largement répandue des algorithmes est connue comme méthode de frontière hiérarchique de volumes. Comme étape de prétraitement, pour chaque objet (dans notre exemple, S et T) nous calculerons une hiérarchie des volumes de frontière. Puis, à chaque temps de l'étape, quand nous devons vérifier les collisions entre S et T, les volumes de frontières hiérarchiques sont employées pour réduire le nombre de paires de triangles à étudier. Au nom de la simplicité, nous donnerons un exemple en utilisant les sphères de frontière, bien qu'on l'ait noté que les sphères sont indésirables dans beaucoup de cas.

Si E est un ensemble de triangles, nous pouvons précalculer une sphère de frontière B(E). Il y a beaucoup de manières de choisir B(E), nous supposons seulement que B(E) est une sphère qui contient complètement E et qui est aussi petit que possible.

En avance, nous pouvons calculer B(S) et B(T). Clairement, si ces deux sphères n'ont pas d'intersection (et c'est très facile à tester), alors ni l'un ni l'autre font S et T. Ce n'est pas bien mieux qu'un algorithme de taillage de n-corps.

Cependant, si E = E₁,E₂,...,E_m est un ensemble de triangles, alors nous pouvons le couper en deux moitiés L(E): = E₁,E₂,...,E_{m / 2} et R(E): = E_{m / 2 + 1},...,E_{m − 1},E_m. Nous pouvons faire ceci à S et à T, puis nous pouvons calculer (en avance) les sphères de frontière B(L(S)),B(R(S)) et B(L(T)),B(R(T)). L'espoir ici est que ces sphères de frontière soient beaucoup plus petites que B(S) et B(T). Et, si, par exemple, B(s) et B(L(t)) n'ont pas d'intersection, alors il n'y a aucun sens à tester n'importe quel triangle dans S contre n'importe quel triangle en L(T).

Comme précalcul, nous pouvons prendre chaque corps physique (représenté par un ensemble de triangles) et le décomposer récursivement dans un arbre binaire, où chaque noeud N représente un ensemble de triangles et ses deux enfants représentent L(N) et R(N). À chaque nœud de l'arbre, en tant que nous précalculons la sphère de frontière B(N).

Quand le moment vient pour tester une paire d'objets pour la collision, leur arbre de sphère frontière peut être employé pour éliminer beaucoup de paires de triangles.

Beaucoup de variantes des algorithmes sont obtenues en choisissant quelque chose autre qu'une sphère pour B(T). Si on choisit les boîtes de frontière axe-alignées, on obtient des arbres AABB. Des arbres de bondissement orientés boîte s'appellent ArbresOBB. Il est plus facile mettre à jour quelques arbres si l'objet fondamental change. Quelques arbres peuvent s'adapter à des primitives d'ordre plus supérieures tels que des cannelures au lieu des simples triangles.

Détection de collision par pair exactes

Une fois que nous avons fait élagage, nous sommes laissés avec un certain nombre de paires de candidates au contrôle pour la détection de collision exacte.

Une observation de base est celle pour deux objets convexes quelconques qui sont disjoints, on peut trouver une surface plane dans l'espace de sorte qu'un objet se trouve complètement d'un côté de cette surface plane et l'autre objet se trouve du côté opposé de cette surface plane. Ceci permet le développement des algorithmes très rapides de détection de collision pour les objets convexes.

Les premiers travaux dans ce secteur ont impliqué  "separating plane" methods  ⇔  des méthodes "de séparation de surfaces planes". Deux triangles se heurtent essentiellement seulement quand ils ne peuvent pas être séparés par une surface plane passant par les trois sommets. C'est-à-dire que si les triangles sont v1,v2,v3 et v4,v5,v6 où chaque vj est un vecteur dans 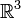, puis nous pouvons prendre trois sommets, vi,vj,vk, trouver une surface plane passer par chacun des trois sommets et vérifier pour voir si c'est une surface plane de séparation. Si une telle surface plane est une surface plane de séparation, alors les triangles sont considérées pour être disjoignent. D'autre part, si aucun de ces avions ne sépare des avions, puis les triangles  are deemed to be disjoint  ⇔  sont considérés pour s'intersecter. Il y a des vingtaines telles surfaces planes.

Si les triangles sont coplanaires, ce test n'est pas entièrement réussi. On peut aussi ajouter quelques surfaces planes supplémentaires, par exemple, des surfaces planes qui sont  normal  ⇔  régularisées aux bords de triangle, pour régler le problème entièrement. Dans d'autres cas, les objets qui se rassemblent face à plat doivent nécessairement également se réunir sous un angle quelque part, par conséquent la détection de collision globale sera capable de trouver la collision.

De meilleures méthodes ont été depuis développées. Des algorithmes très rapides sont disponibles pour trouver les points les plus près sur la surface de deux objets polyédriques convexes. Les premiers travaux par M. C. Lin ^[1] ont employé une variation sur l'algorithme du simplexe de la programmation linéaire. L'algorithme de la distance de Gilbert-Johnson-Keerthi a remplacé cette approche. Ces algorithmes approchent en temps constant où est appliqué à plusieurs reprises aux paires stationnaires ou aux objets bougeant lentement, une fois utilisés avec ces points de départ à partir du précédent contrôle de collision.

traduction à faire

A priori de taillage

traduction à faire

Partitionnement spatiale, divers

traduction à faire

Jeux vidéo

Les jeux vidéo doivent partager leur temps de calcul limité entre plusieurs tâches. Despite this resource limit, and the use of relatively primitive collision detection algorithms, programmers have been able to create believeable, if inexact, systems for use in games.  ⇔  En dépit de ces ressources limitées et de l'utilisation d'algorithmes de détection de collision relativement primitifs, les programmeurs ont été capable de créer des systèmes crédibles, sauf erreur, pour l'utilisation dans les jeux.

Pendant longtemps, les jeux vidéo avaient un nombre limité d'objets à traiter et ainsi la vérification de tous les pairs n'était pas un problème. Dans les jeux bidimensionnels, dans certains cas, le matériel pouvait efficacement détecter et rapporter les pixels de recouvrement entre les sprites sur l'écran. Dans d'autre cas, simplement le carrelage de l'écran et binning de chaque sprite dans les tuiles qu'il recouvre fournit la taille suffisante, et pour des contrôles par paires, des rectangles ou les cercles de bondissement sont employés et considérés suffisamment précis.

Les jeux tridimensionnels ont employé des méthodes de division spatiales pour  n-body pruning  ⇔  n- corps taillant, et pendant longtemps utilisées par un ou quelques sphères objet 3d réel pour par paires des contrôles. Les contrôles exacts sont très rares, excepté dans quelques genres tels que la simulation. Même depuis, des contrôles exacts ne sont pas nécessairement employés dans tous les cas.

Puisque les jeux utilisent une physique simplifié, la stabilité n'est pas beaucoup le but. Presque tous les jeux emploient la détection de collision à posteriori, et les collisions sont souvent résolues en utilisant des règles très simples. Par exemple, si le protagoniste retrouve de lui-même inclut dans un mur, il pourrait être simplement déplacé de nouveau à son dernier bon emplacement connu. Quelques jeux calculeront la distance que le protagoniste peut marcher avant d'être incorporé dans un mur, et lui permettent seulement de se déplacer jusque là.

Un effet légèrement plus sophistiqué et plus saisissant est le modèle physique de ragdoll. Si un personnage de jeu vidéo est mis hors d'action, au lieu du jeu d'une animation prédéfinie, un squelette simplifié du personnage est animé comme si c'étaient une poupée de chiffon. Cette poupée de chiffon tombe mollement, et pourrait se heurter elle-même et l'environnement, dans ce cas elle se comporte convenablement.

Dans beaucoup de cas pour des jeux vidéo, rapprocher les protagonistes par un point est suffisant afin de détecter la collision avec l'environnement. Dans ce cas-ci, les arbres binaires de partitionnement de l'espace fournissent un algorithme simple, efficace et viable pour vérifier si un point est inclus dans le paysage ou pas. Une telle structure de données peut également être employée pour manipuler la situation "de position de repos" avec élégance quand un protagoniste court le long d'une étendue. Des collisions entre les personnages, et les collisions avec des projectiles et les risques, sont traités séparément.

Un simulateur robuste en est un qui réagira à n'importe quelle entrée d'une manière raisonnable. Par exemple, si nous imaginons un jeu vidéo de course de voitures à grande vitesse, d'une étape de simulation à la prochaine, il est imaginable que les voitures avancent une distance substantielle le long du circuit de course. S'il y a un obstacle peu profond sur la voie (telle qu'un mur de brique), il n'est pas entièrement improbable que la voiture le sautera complètement, et cela est très indésirable. Dans d'autres exemples, la "réparation" qu'à posteriori les algorithmes exigent n'est pas mise en application correctement, et les personnages se retrouvent incorporés les murs, ou tombant au loin dans un vide profond de noir. Ce sont les cachets d'une détection de collision et d'un système de simulation physique médiocres.

Références et notes

Voir aussi

• Moteur physique
• Physique informatique