- Des spirales
-
Des spirales (c 225 bc) est un traité d'Archimède. Archimède n'a pas découvert la spirale d'Archimède mais l'utilise dans ce traité pour la quadrature du cercle et la trisection de l'angle[1].
Sommaire
Contenu
Préface
Archimède commence Des Spirales avec un message adressé à Dositheus de Pelusium mentionnant la mort de Conon comme une perte pour les mathématiques. Il résume ensuite les résultats des traités De la sphère et du cylindre et Sur les conoïdes et les sphéroïdes. Il parle ensuite des résultats Des Spirales.
Spirale d'Archimède
Article détaillé : Spirale d'Archimède.
Spirale d'Archimède
La spirale d'Archimède est d'abord étudiée par Conon. Archimède est capable de trouver plusieurs tangentes à la spirale[2]. Il définit la spirale comme :
« Lorsqu’une [demi] droite tourne uniformément dans un plan pendant que l'une de ses extrémités reste fixe et qu'elle revient à sa position initiale, et si sur cette droite en rotation un point se déplace uniformément à partir du point fixe, le point décrira dans le plan une spirale[3]. »
Trisection de l'angle
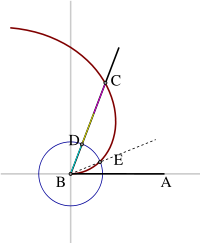
Manière qu'utilise Archimède pour réaliser la trisection de l'angle dans Des Spirales.Pour réaliser la trisection de l'angle, Archimède procède comme suit :
L'angle ABC doit être partagé en trois. Soit le point D tel que BD soit le tiers de BC. Dessiner un cercle de centre et de rayon BD. Le cercle coupe la spirale au point E. L'angle ABE est le tiers de l'angle ABC[4].
Quadrature du cercle
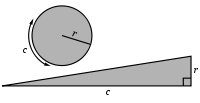
Le cercle et le triangle ont la même aire.Archimède donne les instructions suivantes :
Soit P le point de la spirale de centre O après le premier tour. La tangente à P coupe la ligne perpendiculaire à OP en T. OT est la longueur de la circonférence du cercle de rayon OP.
Archimède a déjà montré dans De la mesure du cercle que "tout cercle équivaut au triangle rectangle pour lequel on a le rayon égal à l'un des côtés adjacents à l'angle droit et le périmètre égal à la base". Donc l'aire du cercle de rayon OP est égal à l'aire du rectangle OPT[5].
Sources
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « On Spirals » (voir la liste des auteurs)
Références
- (en)Spiral, Encyclopædia Britannica, 2008. Consulté le 29 juillet 2008
- (en) Eric W. Weisstein, « Archimedes' Spiral », MathWorld
- André STOLL, « Les spirales », Irem de Strasbourg, 2008, p. 78. Consulté le 12 février 2009
- Tokuda Naoyuki, Chen Liang, « Trisection Angles », Utsunomiya University, Utsunomiya, Japan, 18 mars 1999, p. 5–6. Consulté le 2008-08-20
- History topic: Squaring the circle. Consulté le 20 août 2008
Catégories :- Géométrie euclidienne
- Histoire des mathématiques
- Histoire de la géométrie
- Livre historique de mathématiques
- Littérature de la Grèce antique
Wikimedia Foundation. 2010.
