Corps reel clos

Un corps réel clos est un corps ordonné tel que tout élément positif soit un carré et que tout polynôme de degré impair à coefficients dans F ait au moins une racine dans F.

Le corps des réels, le corps des réels calculables (au sens de Turing) et le corps des algébriques sont des corps réels clos.

Caractérisation des corps réels clos

Un corps réel clos est un corps (commutatif) vérifiant une des conditions suivantes :

1. Il existe un ordre sur F en faisant un corps ordonné tel que, pour cet ordre, tout élément positif de F est un carré dans F, et tout polynôme de degré impair à coefficients dans F admet au moins une racine dans F.
2. F n'est pas algébriquement clos, mais sa clôture algébrique est une extension finie de F.
3. F n'est pas algébriquement clos, mais l'extension 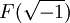est algébriquement close.
4. Il existe un ordre sur F qui ne peut être étendu à aucune extension algébrique de F.
5. Il existe un ordre sur F pour lequel le théorème des valeurs intermédiaires est vrai pour tout polynôme sur F.

La démonstration de ces équivalences n'a rien de simple ; celle de l'implication 1 ⇒ 3 (attribuée par Nicolas Bourbaki à Euler et Lagrange) est donnée dans l'article consacré au théorème de d'Alembert-Gauss

Théorie des corps réels clos

La théorie des corps réels clos est une théorie au premier ordre dont les termes sont des variables, des constantes (entières), des opérations arithmétiques +, -, ×, les formules atomiques des comparaisons entre termes <, ≤, ≥, >, =, ≠ ; les formules sont construites à partir des formules atomiques via les connecteurs ⋀, ⋁, ⇒, et les quantificateurs ∀, ∃.

Cette théorie admet l'élimination des quantificateurs, c'est-à-dire qu'il est possible, à partir d'une formule avec quantificateurs, de trouver une formule équivalente (c'est-à-dire que les deux formules sont vraies pour les mêmes instanciations des variables libres). Il existe des algorithmes procédant à cette élimination. Le premier, dû à Alfred Tarski^[1], avait une complexité non élémentaire, c'est-à-

dire non bornable par une tour d'exponentielles 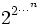, et avait donc un intérêt principalement théorique.

Davenport et Heinz ont montré en 1988 que le problème est intrinsèquement complexe : il existe une famille Φ_n de formules avec n quantificateurs, de longueur O(n) et de degré constant, telle que toute formule sans quantificateur équivalente à Φ_n

doit impliquer des polynômes de degré 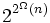et de longueur .

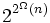Des implémentations d'algorithmes d'élimination des quantificateurs sont fournis par le logiciel QEPCAD et la fonction Reduce de Mathematica 5.^[2]

En raison de l'existence d'algorithmes d'élimination des quantificateurs, la théorie des corps réels clos est décidable : à partir de toute formule close, on peut obtenir algorithmiquement une formule équivalente sans quantificateurs ni variables libres, donc trivialement décidable.

Références

Bibliographie

• Chang, Chen Chung and Keisler, H. Jerome: Model Theory, North-Holland, 1989.
• H. Garth Dales and W. Hugh Woodin: Super-Real Fields, Clarendon Press, 1996.
• Computational Real Algebraic Geometry, Bhubaneswar Mishra, Handbook of Discrete and Computational Geometry, CRC Press, 1997 (Postscript version); also in 2004 edition, p. 743, ISBN 1-58488-301-4
• Saugata Basu, Richard Pollack and Marie-Françoise Roy, Algorithms in real algebraic geometry, Springer, Algorithms and computation in mathematics, 2003, ISBN 3540330984 (online version)
• Bob F. Caviness, Jeremy R. Johnson, éditeurs, Quantifier elimination and cylindrical algebraic decomposition, Springer, 1998, ISBN 3211827943

• Portail des mathématiques