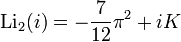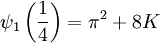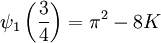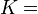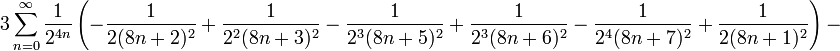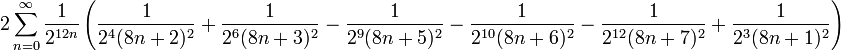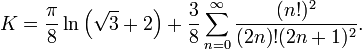- Constante de catalan
-
Constante de Catalan
En mathématiques, la constante de Catalan, nommée d'après le mathématicien Eugène Charles Catalan, est le nombre défini par :
-
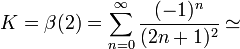 0,91596559417721901505...,
0,91596559417721901505...,
où β est la fonction beta de Dirichlet.
On ne sait pas si la constante K est rationnelle ou irrationnelle et on s'attend à ce qu'elle soit transcendante.
Elle est également égale à :
-
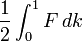 avec
avec 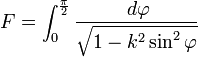
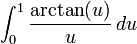
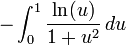

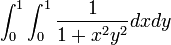
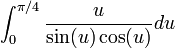
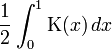
Où K(x) est l'integrale elliptique complète de la première sorte.
Cette constante peut être aussi définie par la fonction de Clausen:
Ce qui nous donne les formules suivantes:
Puisque K est la fonction beta de 2, nous avons donc un lien avec le polylogarithme:
Ou aussi:
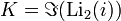 .
.
Sommaire
Utilisation
K apparait en combinatoire, ainsi que dans les valeurs de la fonction polygamma de deuxième ordre, aussi appelée la fonction trigamma:
Simon Plouffe donne une quantité infinie d'identités entre la fonction trigamma, π2 et la constante de Catalan.
Il apparaît aussi dans la distribution sécante hyperbolique.
Séries convergeant rapidement
Les deux formules suivantes convergent rapidement vers K et sont donc ainsi appropriées pour le calcul numérique:
et
Les calculs théoriques pour une telle série sont données par Broadhurst.[1]
Décimales connues
Le nombre de chiffres connus de la constante de Catalan a augmenté radicalement pendant les dernières décennies. Ceci est dû à l'augmentation des performances des ordinateurs et aux améliorations algorithmiques..[2]
Nombres de chiffres connus de la constante de Catalan Date Décimales Calculé par Octobre 2006 5,000,000,000 Shigeru Kondo[3] 2002 201,000,000 Xavier Gourdon & Pascal Sebah 2001 100,000,500 Xavier Gourdon & Pascal Sebah 4 janvier 1998 12,500,000 Xavier Gourdon 1997 3,379,957 Patrick Demichel 1996 1,500,000 Thomas Papanikolaou 29 septembre 1996 300,000 Thomas Papanikolaou 14 août 1996 100,000 Greg J. Fee & Simon Plouffe 1996 50,000 Greg J. Fee 1990 20,000 Greg J. Fee 1913 32 James W. L. Glaisher 1877 20 James W. L. Glaisher Notes et références
- ↑ D.J. Broadhurst, "Polylogarithmic ladders, hypergeometric series and the ten millionth digits of ζ(3) and ζ(5)", (1998) arXiv math.CA/9803067
- ↑ Gourdon, X., Sebah, P; Constants and Records of Computation
- ↑ Shigeru Kondo's website
Lien interne
Bibliographie
- Les nombres remarquables, F. Le Lionnais, Hermann, 1983 puis 1999 (ISBN 2-7056-1407-9)
Catégorie : Constante mathématique -
Wikimedia Foundation. 2010.

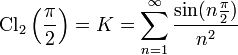
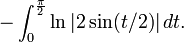
![\frac{\pi}{2}\left[1-\ln\left(\frac{\pi}{2}\right) - \sum_{n=1}^\infty \frac{\zeta(2n)}{n(2n+1)} \left(\frac{1}{4}\right)^n\right]](/pictures/frwiki/100/dae05ad1bbc456cf53f8b30874ad3f9f.png)
![\frac{\pi}{2}\left[3-\ln\left(\frac{15\pi}{32}\right)
-4 \ln \left( \frac{5}{3}\right) +\sum_{n=1}^\infty \frac{\zeta(2n)-1}{n(2n+1)} \left(\frac{1}{4}\right)^n\right]](/pictures/frwiki/102/f1c9dd0c73b3c51972946a2b58290122.png)