Connecteur logique

Un connecteur logique (ou opérateur logique) est, en logique et en linguistique, un symbole ou un mot établissant une liaison entre deux énoncés.

Linguistique

En grammaire, les connecteurs logiques sont des morphèmes (adverbes, conjonctions de coordination ou de subordination, parfois même interjections), qui établissent une liaison entre deux énoncés, voire entre un énoncé et une énonciation. Ils regroupent des connecteurs logiques et des connecteurs argumentatifs comme «mais», c'est-à-dire des mots qui, en plus de leur rôle de jonction, insèrent les énoncés reliant dans un cadre argumentatif. L'étude des connecteurs intègre ainsi les perspectives de la grammaire de texte (soucieuse de la cohésion du texte) et celle de la pragmatique (intéressé par l'orientation argumentative des énoncés et la relation d'interlocution).

L'absence de connecteur entre deux énoncés est en soi une forme de jonction.

On peut citer les connecteurs suivants :

• Addition : et, de plus, puis, en outre, non seulement ... mais encore, de surcroît, ainsi que, également
• Alternative : ou, soit ... soit, tantôt ... tantôt, ou ... ou, ou bien, seulement ... mais encore, l'un ... l'autre, d'un côté ... de l'autre
• But : afin que, pour que, de peur que, en vue que, de façon à ce que
• Cause : car, en effet, effectivement, comme, par, parce que, puisque, attendu que, vu que, étant donné que, grâce à, à cause de, par suite de, en égard à, en raison de, du fait que, dans la mesure où, sous prétexte que
• Comparaison : comme, de même que, ainsi que, autant que, aussi ... que, si ... que, de la même façon que, semblablement, pareillement, plus que, moins que, non moins que, selon que, suivant que, comme si
• Concession : malgré, en dépit de, quoique, bien que, alors que, quel que soit, même si, ce n'est pas que, certes, bien sûr, évidemment, il est vrai que, toutefois
• Conclusion : en conclusion, pour conclure, en guise de conclusion, en somme, bref, ainsi, donc, en résumé, en un mot, par conséquent, finalement, enfin, en définitive
• Condition, supposition : si, au cas où, à condition que, pourvu que, à moins que, en admettant que, pour peu que, à supposer que, en supposant que, dans l'hypothèse où, dans le cas où, probablement, sans doute, apparemment
• Conséquence : donc, aussi, partant, alors, ainsi, ainsi donc, par conséquent, si bien que, d'où, en conséquence, conséquemment, par suite, c'est pourquoi, de sorte que, en sorte que, de façon que, de manière que, si bien que, tant et si bien que
• Classification, énumération : d'abord, tout d'abord, de prime abord, en premier lieu, premièrement, en deuxième lieu, en second lieu, deuxièmement, après, ensuite, de plus, quant à, en troisième lieu, puis, en dernier lieu, pour conclure, enfin
• Explication : savoir, à savoir, c'est-à-dire, soit
• Illustration : par exemple, comme ainsi, c'est ainsi que, c'est le cas de, notamment, entre autres, en particulier, à l'image de, comme l'illustre, comme le souligne, tel que
• Justification : car, c'est-à-dire, en effet, parce que, puisque, en sorte que, ainsi, c'est ainsi que, non seulement ... mais encore, du fait de
• Liaison : alors, ainsi, aussi, d'ailleurs, en fait, en effet, de surcroît, de même, également, puis, ensuite, de plus,en outre
• Opposition : mais, cependant, or, en revanche, alors que, pourtant, par contre, tandis que, néanmoins, au contraire, pour sa part, d'un autre côté, en dépit de, malgré, au lieu de, d'une part...d'autre part
• Restriction : cependant, toutefois, néanmoins, pourtant, mis à part, ne ... que, en dehors de, hormis, à défaut de, excepté, sauf, uniquement, simplement
• Temps : quand, lorsque, comme, avant que, après que, alors que, dès lors que, depuis que, tandis que, en même temps que, pendant que, au moment où

Logique formelle

En toute généralité une logique p-valente possède connecteurs n-aires.

Table des connecteurs logiques.

Connecteurs logiques organisés en un diagramme de Hasse.

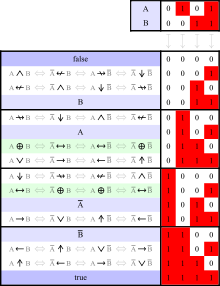
Dans le cas de la logique bivalente classique le tableau suivant recense les seize fonctions booléennes associées aux entrées P et Q.

Connecteur	Notation	Formules équivalentes	Table de vérité	Diagramme de Venn
Contradiction		P ¬P	Q 0 1 P 0   0 0 1   0 0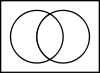
Conjonction (ET)	P Q P & Q P · Q P AND Q	P ¬Q ¬P Q ¬P ¬Q	Q 0 1 P 0   0 0 1   0 1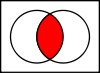
Non-implication réciproque	P Q P Q	P ↓ ¬Q ¬P & Q ¬P ¬Q	Q 0 1 P 0   0 1 1   0 0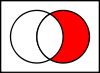
Proposition Q	Q		Q 0 1 P 0   0 1 1   0 1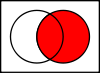
Non-implication	P Q P Q	P & ¬Q ¬P ↓ Q ¬P ¬Q	Q 0 1 P 0   0 0 1   1 0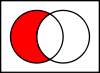
Proposition P	P		Q 0 1 P 0   0 0 1   1 1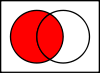
Disjonction exclusive (OU exclusif)	P Q P Q P Q P XOR Q	P ¬Q ¬P Q ¬P ¬Q	Q 0 1 P 0   0 1 1   1 0
Disjonction (OU)	P Q P ∨ Q P OR Q	P ¬Q ¬P → Q ¬P ↑ ¬Q	Q 0 1 P 0   0 1 1   1 1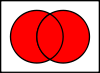
Disjonction réciproque (NON-OU)	P ↓ Q P NOR Q	P ¬Q ¬P Q ¬P & ¬Q	Q 0 1 P 0   1 0 1   0 0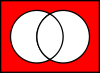
Équivalence	P Q P ≡ Q P XNOR Q P IFF Q	P ¬Q ¬P Q ¬P ¬Q	Q 0 1 P 0   1 0 1   0 1
Négation de P	¬P ~P		Q 0 1 P 0   1 1 1   0 0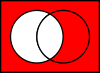
Implication	P → Q P Q	P ↑ ¬Q ¬P Q ¬P ← ¬Q	Q 0 1 P 0   1 1 1   0 1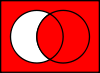
Négation de Q	¬Q ~Q		Q 0 1 P 0   1 0 1   1 0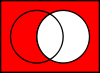
Implication réciproque	P Q P Q	P ¬Q ¬P ↑ Q ¬P → ¬Q	Q 0 1 P 0   1 0 1   1 1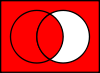
NON-ET	P ↑ Q P | Q P NAND Q	P → ¬Q ¬P ← Q ¬P ¬Q	Q 0 1 P 0   1 1 1   1 0
Tautologie		P ¬P	Q 0 1 P 0   1 1 1   1 1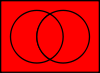

Annexes

Liens internes

• Mot
• Syntaxe
• Nature (grammaire)
• Syntagme
• Fonction syntaxique
• Analyse morphosyntaxique
• Représentation (grammaire)
• Énonciation
• Liste des notions utilisées en linguistique

Liens externes

• Les connecteurs logiques (exercices interactifs) sur le site Magister. Attention, dans ces exercices, la correction est identifiée au texte original, ce qui traite comme erreurs, même s'ils produisent des textes corrects, les autres connecteurs ou organisations de textes.
• Tableau des connecteurs logiques. On peut y trouver des conjonctions de coordination, des adverbes, des locutions adverbiales, ainsi que des conjonctions et locutions conjonctives de subordination !!

• Portail de la linguistique
• Portail de la logique