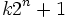Conjecture du problème de Sierpinski

Conjecture du problème de Sierpinski

Nombre de Sierpiński

En mathématiques, un nombre de Sierpinski est un nombre positif, impair k tel que les entiers de la forme

k2^{n} + 1\,\!

sont composés (c.a.d. non premier) pour tous les nombres naturels n.

En 1960 Wacław Sierpiński montra qu'il existe une infinité de ces nombres.

En 1962, ayant trouvé que 78 557 = 17 x 4621 est un nombre de Sierpinski, John Selfridge conjectura que 78 557 était le plus petit de ces nombres.

Pour montrer que 78 557 est réellement le plus petit nombre de Sierpinski, il suffit pour chaque nombre impair plus petit de trouver un exposant n tel que (k. 2^n +1) soit premier. En 2000, il ne restait plus que dix-sept candidats possibles.

Seventeen or Bust, (Dix-sept ou arrêt) le projet de calcul distribué, commença à tester ces dix-sept nombres pour voir s'ils pouvaient être éliminés de la liste des nombres de Sierpinski possibles. Si le projet trouve que tous ces nombres génèrent un nombre premier, le projet aura trouvé une preuve de la conjecture de Selfridge.

Le projet réussit à trouver onze nombres premiers supplémentaires ; en conséquence, il ne reste plus que six k à tester. Le 11ième a été trouvé en octobre 2007.

Exemple : le nombre 78557

John Selfridge prouva en 1962 que 78557 est un nombre de Sierpiński.

La preuve montre que tout choix de n rentre dans au moins une catégorie parmi 7, où chaque catégorie garantit un facteur pour N.

Selfridge prouva en effet que :

  • 78557 * 22n + 1 est un multiple de 3
  • 78557 * 24n + 1 + 1 est un multiple de 5
  • 78557 * 23n + 1 + 1 est un multiple de 7
  • 78557 * 212n + 11 + 1 est un multiple de 13
  • 78557 * 218n + 15 + 1 est un multiple de 19
  • 78557 * 236n + 27 + 1 est un multiple de 37
  • 78557 * 29n + 3 + 1 est un multiple de 73

Ainsi l'on peut construire la table des exposants modulo 36 :

Si l'exposant est congru à ... modulo 36 alors N a pour diviseur...
0 3
1 5
2 3
3 73
4 3
5 5
6 3
7 7
8 3
9 5
10 3
11 13
12 3
13 5
14 3
15 19
16 3
17 5
18 3
19 7
20 3
21 5
22 3
23 13
24 3
25 5
26 3
27 37
28 3
29 5
30 3
31 7
32 3
33 5
34 3
35 13

Ainsi tous les exposants sont considérés, ce qui veut dire qu'aucun membre de la séquence ne peut être premier. On peut dire la même chose des nombres 271129, 271577, 322523, 327739, 482719, 575041, 603713, 903983, 934909, 965431, 1259779, 1290677, 1518781, 1624097, 1639459, 1777613, 2131043, etc.

Voir aussi

  • Portail des mathématiques Portail des mathématiques
Ce document provient de « Nombre de Sierpi%C5%84ski ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Conjecture du problème de Sierpinski de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Conjecture du problème de Sierpiński — Nombre de Sierpiński En mathématiques, un nombre de Sierpinski est un nombre positif, impair k tel que les entiers de la forme sont composés (c.a.d. non premier) pour tous les nombres naturels n. En 1960 Wacław Sierpiński montra qu il existe une… …   Wikipédia en Français

  • Problème de Sierpiński — Nombre de Sierpiński En mathématiques, un nombre de Sierpinski est un nombre positif, impair k tel que les entiers de la forme sont composés (c.a.d. non premier) pour tous les nombres naturels n. En 1960 Wacław Sierpiński montra qu il existe une… …   Wikipédia en Français

  • Sierpinski — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot Sierpinski peut renvoyer à : Wacław Sierpiński, mathématicien polonais Tapis de Sierpiński Tapis de Sierpiński (programme informatique)… …   Wikipédia en Français

  • Premier problème de Hilbert — Hypothèse du continu En théorie des ensembles, l hypothèse du continu, due à Georg Cantor, affirme qu il n existe aucun ensemble dont le cardinal est strictement compris entre le cardinal de l ensemble des entiers naturels et celui de l ensemble… …   Wikipédia en Français

  • Sierpinsky — Sierpinski Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Le mot Sierpinski peut renvoyer à : Wacław Sierpiński, mathématicien polonais Tapis de Sierpiński Tapis de Sierpiński (programme… …   Wikipédia en Français

  • Dix-sept ou arrêt — Seventeen or Bust « Seventeen or Bust » (Dix sept ou arrêt) est un projet de calcul distribué, pour résoudre le problème de Sierpiński. Le but de ce projet est de prouver que 78 557 est le plus petit nombre de Sierpiński. Pour ce faire …   Wikipédia en Français

  • Seventeen or Bust — « Seventeen or Bust » (Dix sept ou arrêt) est un projet de calcul distribué, pour résoudre le problème de Sierpiński. Le but de ce projet est de prouver que 78 557 est le plus petit nombre de Sierpiński. Pour ce faire, tous les nombres… …   Wikipédia en Français

  • Seventeen or bust — « Seventeen or Bust » (Dix sept ou arrêt) est un projet de calcul distribué, pour résoudre le problème de Sierpiński. Le but de ce projet est de prouver que 78 557 est le plus petit nombre de Sierpiński. Pour ce faire, tous les nombres… …   Wikipédia en Français

  • Nombres 10 000 a 99 999 — Nombres 10 000 à 99 999 Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de dix mille (10 000) à quatre vingt dix neuf mille neuf cent quatre vingt dix neuf (99 999). Article détaillé : 10 000 (nombre).… …   Wikipédia en Français

  • Nombres 10 000 À 99 999 — Cet article recense la plupart des nombres qui ont des propriétés remarquables allant de dix mille (10 000) à quatre vingt dix neuf mille neuf cent quatre vingt dix neuf (99 999). Article détaillé : 10 000 (nombre). Sommaire 1 Nombres dans l …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”