Congrus
- Congrus
-
Congruence

Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom.
Derrière le terme de congruence se cachent des notions semblables mais de niveaux d'abstraction différents. Historiquement, la notion de congruence sur les entiers relatifs a été introduite par Gauss vers 1801.[1]
- Dans la mesure des angles orientés, on dit que deux mesures sont congrues modulo 2π si et seulement si leur différence est un multiple de 2π. Cela caractérise deux mesures d'un même angle.
- En algèbre, on parle
- de congruence modulo I dans un anneau commutatif (R, +, *) dont I est un idéal :
- x est congru à y modulo I si et seulement si x - y appartient à I.
- Cette congruence est une relation d'équivalence, compatible avec les opérations + et * et permet de définir un anneau quotient R/I.
- Les deux notions précédentes deviennent alors des cas particuliers de cette définition plus générale.
- de congruence modulo H dans un groupe G quand H est un sous-groupe de G.
- x est congru à y modulo H si et seulement si
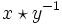 appartient à H.
appartient à H.
- Cette relation est une relation d'équivalence permettant de construire un ensemble quotient qui, si H est un sous-groupe distingué, est un groupe quotient
- de congruence dans un semi-groupe (G,*) pour toute relation d'équivalence compatible avec la loi *. Cette définition est alors plus large que la précédente mais on ne parle alors plus de congruence modulo ...
- En géométrie riemannienne, une congruence est l'ensemble des courbes intégrales associées à un champ de vecteurs.
- On trouve parfois, dans des ouvrages inspirés de la langue anglo-saxonne, le terme de congru mis à la place de semblable. Il s'agit alors d'une simple relation d'équivalence sur l'ensemble des figures planes.
- En psychothérapie, congruence est le terme employé par Carl Rogers pour indiquer une correspondance exacte entre l'expérience et la prise de conscience.
- En sciences humaines et sociales et notamment en géographie la congruence est "l'adaptation réciproque".[2]
- En anatomie, on parle de congruence des surfaces articulaires. Deux surfaces sont congruentes lorsque il y a un emboitement parfait, c'est le cas de l'articulation coxo-fémoral. Contrairement à l'articulation du genou où les surfaces articulaires sont rendues congruentes par les ménisques.
- ↑ TLFI ou Petite encyclopédie des mathématiques p 729
- ↑ lu dans M Cohou in Le destin d'un voie rapide Ed PUM
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Congrus de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
NOMBRES (THÉORIE DES) - Nombres algébriques — Les mathématiciens grecs avaient découvert que certains rapports de grandeurs ne sont pas rationnels, c’est à dire qu’ils ne sont pas égaux au rapport de deux entiers: il en est ainsi du rapport de la diagonale d’un carré à son côté, puisque… … Encyclopédie Universelle
Théorème des deux carrés de Fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut … Wikipédia en Français
congru — congru, ue [ kɔ̃gry ] adj. • fin XIIIe; lat. congruus « convenable » 1 ♦ Vx Qui convient exactement à une situation donnée. ⇒ adéquat, convenable, pertinent. « Après une attente congrue dans les salons » (France). 2 ♦ (1615) PORTION CONGRUE : vx… … Encyclopédie Universelle
Nombres premiers somme de 2 carrés — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… … Wikipédia en Français
Theoreme des deux carres de Fermat — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… … Wikipédia en Français
Théorème de Fermat sur les sommes de deux carrés — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… … Wikipédia en Français
Théorème des deux carrés — de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons… … Wikipédia en Français
Théorème des deux carrés de fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut … Wikipédia en Français
Disquisitiones Arithmeticae — Couverture de la première édition. Disquisitiones Arithmeticae est un livre de théorie des nombres écrit par le mathématicien allemand Carl Friedrich Gauss. Sa première publication date de 1801. Dans ce livre, Gauss réorganise le domaine en… … Wikipédia en Français
Disquisitiones arithmeticae — Couverture de la première édition. Disquisitiones Arithmeticae est un livre de théorie des nombres écrit par le mathématicien allemand Carl Friedrich Gauss. Sa première publication date de 1801. Dans ce livre, Gauss réorganise le domaine en… … Wikipédia en Français
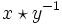 appartient à H.
appartient à H.