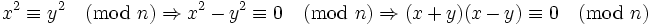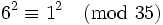Congruence de carres

Congruence de carres

Congruence de carrés

En arithmétique modulaire, une congruence de carrés modulo un entier n est une égalité telle que

x^2\equiv y^2 \pmod{n}\hbox{ avec }x\not\equiv \pm y\pmod{n}.

Un tel rapport porte des informations utiles dans l'essai de factorisation l'entier n : résoudre une congruence de carrés modulo n est un chose recherchée après une factorisation d'entier. Ce qui en découle

x^2\equiv y^2\pmod{n} \Rightarrow x^2-y^2\equiv 0\pmod{n} \Rightarrow (x+y)(x-y)\equiv 0\pmod{n}

Ceci veut dire que n divise (x+y)(x−y) mais pas (x+y) ou (x−y) tout seul, donc (x+y) et (x−y), tous les deux, contiennent des facteurs de n. Une simple opération de PGCD extraira un facteur dans la plupart des cas. La difficulté réside dans la recherche de x et y. Ceci, incidemment, est ce que font ensemble le crible quadratique et le crible de corps de nombre : établir une congruence de carrés modulo n. Cette approche de la factorisation montre aussi que le problème de la factorisation peut être réduit au problème de recherche de racines carrées modulo n.

Un cas où une congruence de carrés ne donnera pas un facteur est quand seulement une partie du produit de la paire (x+y) ou (x-y) partage un facteur avec n. Ceci implique que la partie qui partage les facteurs avec n est soit égale à n ou à un multiple de n. Le pgcd de cette partie et n sera aussi n, et le pgcd de n et de l'autre partie sera 1. Pour pouvoir extraire n'importe quel facteur de la congruence de carrés, les deux parties (x+y) et (x-y) doivent chacune partager au moins un facteur avec n.

Voici un exemple. Prenons n = 35. Le carré parfait le plus proche de 35 est 36, et, 36 ≡ 1 (mod 35). Comme 1 est aussi un carré parfait, nous avons notre congruence :

6^2\equiv 1^2\pmod{35}

avec pgcd(6 + 1, 35) = 7 et pgcd(6 - 1, 35) = 5. Ceux-ci sont les deux facteurs non triviaux de 35.

Ce document provient de « Congruence de carr%C3%A9s ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Congruence de carres de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

  • Congruence De Carrés — En arithmétique modulaire, une congruence de carrés modulo un entier n est une égalité telle que . Un tel rapport porte des informations utiles dans l essai de factorisation l entier n : résoudre une congruence de carrés modulo n est un… …   Wikipédia en Français

  • Congruence de carrés — En arithmétique modulaire, une congruence de carrés modulo un entier n est une équation de la forme Utilisation Une telle équation apporte des informations utiles pour essayer de factoriser l entier n. En effet, Ceci veut dire que n divise le… …   Wikipédia en Français

  • Nombres premiers somme de 2 carrés — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… …   Wikipédia en Français

  • Theoreme des deux carres de Fermat — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… …   Wikipédia en Français

  • Théorème de Fermat sur les sommes de deux carrés — Théorème des deux carrés de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de… …   Wikipédia en Français

  • Théorème des deux carrés — de Fermat Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons… …   Wikipédia en Français

  • Théorème des deux carrés de Fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut …   Wikipédia en Français

  • Théorème des deux carrés de fermat — Pierre Fermat En mathématiques, le théorème des deux carrés de Fermat énonce les conditions pour qu’un nombre entier soit la somme de deux carrés parfaits (c est à dire de deux carrés d’entiers) et précise de combien de façons différentes il peut …   Wikipédia en Français

  • Théorème des quatre carrés de Lagrange — Le théorème des quatre carrés de Lagrange, est également connu sous le nom de conjecture de Bachet  ; il a été énoncé pour la première fois par Claude Gaspard Bachet de Méziriac en 1621, dans les notes accompagnant sa traduction en latin du… …   Wikipédia en Français

  • Crible Quadratique — L algorithme crible quadratique (QS pour Quadratic sieve) est un algorithme moderne de décomposition en produit de facteurs premiers fondé sur l arithmétique modulaire. Dans la pratique, la seconde méthode connue la plus rapide. C est un… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”