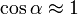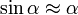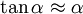Condition de Gauss
- Condition de Gauss
-
Approximation de Gauss
L'approximation de Gauss (d'après le physicien allemand Carl Friedrich Gauss) est l'approximation linéaire de l'optique géométrique[1] obtenue lorsque les angles d'incidence des rayons sont faibles et que le point d'incidence est proche de l'axe optique. Les écarts à cette approximation (rencontrés notamment dans les instruments d'optique travaillant en « grand angle ») sont appelés aberrations géométriques.
L'ensemble des conditions menant à l'approximation de Gauss est appelé conditions de Gauss.
Conséquences mathématiques
L'approximation des petits angles permet, au premier ordre, la linéarisation des fonctions trigonométriques de base :
Notes et références de l'article
- ↑ José-Philippe Pérez, Optique : Fondements et applications, [détail des éditions], 5e édition, page 28.
Voir aussi
Articles connexes
 Portail de la physique
Portail de la physique
Catégorie : Optique géométrique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Condition de Gauss de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Gauss–Markov theorem — This article is not about Gauss–Markov processes. In statistics, the Gauss–Markov theorem, named after Carl Friedrich Gauss and Andrey Markov, states that in a linear model in which the errors have expectation zero and are uncorrelated and have… … Wikipedia
Gauss–Kuzmin–Wirsing operator — GKW redirects here. For the Indian engineering firm see Guest Keen Williams.In mathematics, the Gauss–Kuzmin–Wirsing operator occurs in the study of continued fractions; it is also related to the Riemann zeta function. IntroductionThe… … Wikipedia
Gauss–Codazzi equations — In Riemannian geometry, the Gauss–Codazzi–Mainardi equations are fundamental equations in the theory of embedded hypersurfaces in a Euclidean space, and more generally submanifolds of Riemannian manifolds. They also have applications for embedded … Wikipedia
Gauss's lemma (number theory) — This article is about Gauss s lemma in number theory. Gauss s lemma (polynomial) concerns factoring polynomials. Gauss s lemma in number theory gives a condition for an integer to be a quadratic residue. Although it is not useful computationally … Wikipedia
Gauss–Seidel method — The Gauss–Seidel method is a technique used to solve a linear system of equations. The method is named after the German mathematicians Carl Friedrich Gauss and Philipp Ludwig von Seidel. The method is an improved version of the Jacobi method. It… … Wikipedia
Théorème de Gauss-Wantzel — Pour les articles homonymes, voir Théorème de Gauss et Théorème de Wantzel. En géométrie, le théorème de Gauss Wantzel énonce une condition nécessaire et suffisante pour qu un polygone régulier soit constructible à la règle et au compas. Sommaire … Wikipédia en Français
Nombre Premier De Gauss — Ouvrage traitant des entiers de Gauss 1801. En mathématiques et plus précisément en algèbre, un nombre premier de Gauss est une notion de théorie algébrique des nombres concernant les entiers de Gauss. Un nombre premier de Gauss correspond au… … Wikipédia en Français
Nombre premier de Gauss — Ouvrage traitant des entiers de Gauss 1801. En mathématiques et plus précisément en algèbre, un nombre premier de Gauss est une notion de théorie algébrique des nombres concernant les entiers de Gauss. Un nombre premier de Gauss correspond au… … Wikipédia en Français
Nombre premier de gauss — Ouvrage traitant des entiers de Gauss 1801. En mathématiques et plus précisément en algèbre, un nombre premier de Gauss est une notion de théorie algébrique des nombres concernant les entiers de Gauss. Un nombre premier de Gauss correspond au… … Wikipédia en Français
Theoreme de Gauss-Wantzel — Théorème de Gauss Wantzel Pour les articles homonymes, voir Théorème de Gauss. En géométrie, le théorème de Gauss Wantzel précise la condition nécessaire et suffisante pour qu un polygone régulier soit constructible à la règle et au compas.… … Wikipédia en Français