Classe caracteristique
- Classe caracteristique
-
Classe caractéristique
En topologie algébrique, les classes caractéristiques sont des invariants cohomologiques des fibrés vectoriels, répondant à une tentative de classification. Plus précisément, si 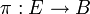 est un fibré vectoriel, une classe caractéristique de π est une classe c(π) dans la cohomologie de la base B qui vérifie la condition de compatibilité suivante:
est un fibré vectoriel, une classe caractéristique de π est une classe c(π) dans la cohomologie de la base B qui vérifie la condition de compatibilité suivante:
Si 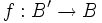 est une application continue, alors :
est une application continue, alors :
c(f * (π)) = f * (c(π))
où f * (π) est le fibré vectoriel induit sur B' par f.
Exemples
- Classe d'Euler
- Classe de Stiefel-Whitney pour les fibrés vectoriels réels.
- Classe de Chern pour les fibrés vectoriels complexes.
- Classe de Pontrjagin pour les fibrés réels, elles sont construites à partir des classes de Chern du fibré complexifié.
 Portail des mathématiques
Portail des mathématiques
Catégories : Invariant | Homologie | Classe caractéristique
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Classe caracteristique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Classe Caractéristique — En topologie algébrique, les classes caractéristiques sont des invariants cohomologiques des fibrés vectoriels, répondant à une tentative de classification. Plus précisément, si est un fibré vectoriel, une classe caractéristique de π est une… … Wikipédia en Français
Classe caractéristique — En topologie algébrique, les classes caractéristiques sont des invariants cohomologiques des fibrés vectoriels, répondant à une tentative de classification. Plus précisément, si est un fibré vectoriel, une classe caractéristique de π est une… … Wikipédia en Français
Classe De Stiefel-Whitney — En géométrie, les classes de Stiefel Whitney sont des classes caractéristiques associées aux fibrés vectoriels réels de rang fini. Elles constituent donc un analogue réel des classes de Chern dans le cas complexe. Elle portent le nom de Hassler… … Wikipédia en Français
Classe de Stiefel-Withney — Classe de Stiefel Whitney En géométrie, les classes de Stiefel Whitney sont des classes caractéristiques associées aux fibrés vectoriels réels de rang fini. Elles constituent donc un analogue réel des classes de Chern dans le cas complexe. Elle… … Wikipédia en Français
Classe de stiefel-whitney — En géométrie, les classes de Stiefel Whitney sont des classes caractéristiques associées aux fibrés vectoriels réels de rang fini. Elles constituent donc un analogue réel des classes de Chern dans le cas complexe. Elle portent le nom de Hassler… … Wikipédia en Français
Classe de Stiefel-Whitney — En géométrie, les classes de Stiefel Whitney sont des classes caractéristiques associées aux fibrés vectoriels réels de rang fini. Elles constituent donc un analogue réel des classes de Chern dans le cas complexe. Elle portent le nom de Hassler… … Wikipédia en Français
classe — [ klas ] n. f. • 1355; lat. classis I ♦ Dans un groupe social, Ensemble des personnes qui ont en commun une fonction, un genre de vie, une idéologie, etc. ⇒ caste, catégorie, clan, état, 1. gent, groupe, ordre. 1 ♦ Antiq. Chacune des catégories… … Encyclopédie Universelle
caractéristique — [ karakteristik ] adj. et n. f. • 1550; gr. kharaktêristikos I ♦ Adj. 1 ♦ Qui constitue un élément distinctif reconnaissable. Différence, élément, marque, propriété, signe, trait caractéristique. ⇒ déterminant, distinctif, essentiel, particulier … Encyclopédie Universelle
Classe Sa'ar IV — Autres noms classe Reshef Histoire Commanditaire … Wikipédia en Français
Classe Préparatoire Aux Grandes Écoles — Les classes préparatoires aux grandes écoles (CPGE) sont des filières d enseignement supérieur situées généralement dans les lycées. Communément appelées classes prépas ou prépas et pour la plupart publiques, elles sélectionnent sur dossier et… … Wikipédia en Français
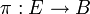 est un fibré vectoriel, une classe caractéristique de π est une classe c(π) dans la cohomologie de la base B qui vérifie la condition de compatibilité suivante:
est un fibré vectoriel, une classe caractéristique de π est une classe c(π) dans la cohomologie de la base B qui vérifie la condition de compatibilité suivante: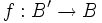 est une application continue, alors :
est une application continue, alors :