Classe de Stiefel-Withney

En géométrie, les classes de Stiefel-Whitney sont des classes caractéristiques associées aux fibrés vectoriels réels de rang fini.

Elles constituent donc un analogue réel des classes de Chern dans le cas complexe.

Elle portent le nom de Hassler Whitney et de Eduard Stiefel.

Toute classe caractéristique associée aux fibrés vectoriels réels apparait comme un polynôme en les classes de Stiefel-Withney.

Axiomatique

On montre le résultat suivant:

Pour tout fibré vectoriel 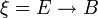, il existe des classes de cohomologie 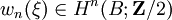, , 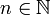vérifiant les axiomes suivants :

• w₀(ξ) = 1

• w_n(ξ) = 0 pour n strictement supérieur à la dimension des fibres.

• Si 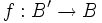est une application continue, alors :

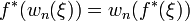
• Si on note 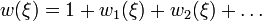, alors :

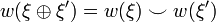où 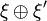désigne la somme de Whitney des fibrés ξ et ξ'

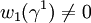• où γ¹ désigne le fibré canonique sur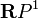

Remarques

La troisième condition assure que les classes de Stiefel-Whitney d'un fibré trivial sont nulles (sauf celle d'indice 0). En effet un fibré trivial est isomorphe à l'image réciproque d'un fibré sur le point. Malheureusement, la réciproque de cette proposition est fausse. Par exemple, on peut montrer que les fibrés tangents sur la sphère de dimension 2 a toutes ses classes de Stiefel-Whitney nulles mais ce fibré est non trivial.

La dernière condition assure que les classes ne sont pas triviales. En effet, si on retirait cette condition, on pourrait poser w_i(ξ) = 0 pour tout .

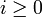Classification des classes caractéristiques

Cohomologie des grassmanniennes

• Portail des mathématiques