Cercles Orthogonaux

Cercle orthogonal

Deux cercles sécants dans un plan sont dits orthogonaux si en chacun des deux points d'intersection les tangentes à l'un et à l'autre cercle sont orthogonales. Par raison de symétrie, il suffit que la propriété précédente ait lieu en un des points d'intersection. D'autre part, chaque tangente précitée à l'un des cercles passe par le centre de l'autre.

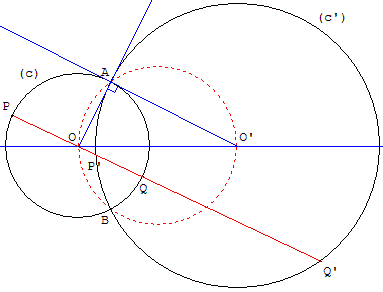
La figure formée par les deux centres O, O' et un des deux points d'intersection est un triangle rectangle. Par le théorème de Pythagore, il en résulte la relation entre les deux rayons et la distance entre les centres : OO' ² = R ² + R' ².

Réciproquement, si deux cercles sont sécants et vérifient cette relation ils sont orthogonaux.

Pour que deux cercles soient orthogonaux, il faut et il suffit qu'il existe un diamètre de l'un d'entre eux qui soit divisé harmoniquement par l'autre. En effet la puissance du point O par rapport au cercle (c') est OA² = OP' × OQ'. On a donc OP² = OQ² = OP' × OQ'.
[P, Q, P', Q'] est une division harmonique d'après la relation de Newton.

Application : étant donné un cercle (c) et un point M, distinct du centre O et n'appartenant pas au cercle, pour trouver les cercles orthogonaux à (c) passant par M, tracer le diamètre [PQ] sur la droite (OM) et trouver le point M' tel que [P, Q, M, M'] soit une division harmonique :
.
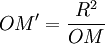Tout cercle passant par M et M', centré sur la médiatrice de [MM'], est orthogonal à (c).
L'ensemble des cercles passant par M et orthogonaux à (c) est un faisceau de cercles à points de base M et M'.

Cercle orthogonal à trois cercles (de centres non alignés)

C'est le cercle dont le centre O est le centre radical des trois cercles et dont le rayon est égal à la racine de la puissance p du point O par rapport à l'un des trois cercles. Si O est à l'intérieur des cercles, p est négatif, le problème n'a pas de solution dans le plan métrique réel.

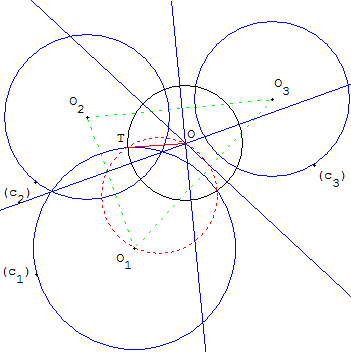
Faisceaux orthogonaux

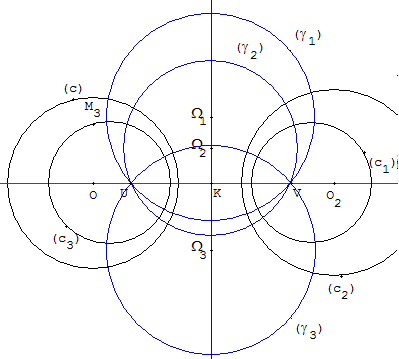
Étant donné deux cercles (c) et (c₁) non concentriques, il existe une infinité de cercles (γ) orthogonaux à (c) et (c₁), ils sont aussi orthogonaux à tous les cercles du faisceau déterminé par (c) et (c₁).

Les cercles (γ) orthogonaux aux cercles (c) d'un faisceau F forment un faisceau Φ conjugué de F. L'axe radical d'un des faisceaux est la droite des centres de l'autre.
Si l'un des faisceaux est formé de cercles tangents, il en est de même de l'autre. Sinon si l'un des faisceaux est à points de base, l'autre est à points limites, et il y a identité entre ces couples de points.

Articles connexes et lien externe

• Cercle
• Puissance d'un point par rapport à un cercle
• Faisceau de cercles

Voir des applications dans "avec GéoPlan" : la géométrie du cercle

• Portail de la géométrie