Inscrit (géométrie)
- Inscrit (géométrie)
-
Cercle inscrit
En géométrie, un cercle inscrit à un polygone est un cercle qui est tangent à tous les côtés de ce polygone. De manière plus générale, on parle de cercle inscrit dans une surface bornée pour indiquer un cercle de plus grand rayon possible inclus dans la surface.
Existence
Pour qu'un polygone possède un cercle inscrit, il faut que ses bissectrices soient concourantes. Si c'est le cas, le point d'intersection désigne le centre du cercle inscrit. On peut alors trouver le rayon de ce cercle en traçant la perpendiculaire a un segment du cercle et passant par le point d'intersection des bissectrices.
Cas particuliers
Triangle
Tout triangle non plat possède un unique cercle inscrit.
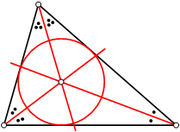
Cercle inscrit dans un triangle
Voir aussi
 Portail de la géométrie
Portail de la géométrie
Catégories : Géométrie du triangle | Cercle et sphère
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Inscrit (géométrie) de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
GÉOMÉTRIE — La géométrie est communément définie comme la science des figures de l’espace. Cette définition un peu incertaine risque de conduire à inclure dans la géométrie des questions qui ne sont géométriques que dans leur langage, mais relèvent en fait… … Encyclopédie Universelle
Géométrie en Égypte antique — Géométrie dans l Égypte antique Cet article fait partie de la série Sciences dans l Égypte antique Mathématiques Géométrie Unités de mesure Chiffres Fraction … Wikipédia en Français
Geometrie projective — Géométrie projective La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques … Wikipédia en Français
Géométrie Projective — La géométrie projective est le domaine des mathématiques qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés des figures inchangées par projection. Sommaire 1 Considérations historiques 2 Aperçu élémentaire … Wikipédia en Français
Géometrie à 366 degrés — Géométrie mégalithique Stonehenge Géométrie mégalithique (également appelée géométrie à 366 degrés) est le nom donné à une hypothétique science géométrique, supposée avoir été utilisée et peut être créée par la civilisation mégalithique de Grande … Wikipédia en Français
Géométrie à 366 degrés — Géométrie mégalithique Stonehenge Géométrie mégalithique (également appelée géométrie à 366 degrés) est le nom donné à une hypothétique science géométrique, supposée avoir été utilisée et peut être créée par la civilisation mégalithique de Grande … Wikipédia en Français
Géométrie dans l'Égypte antique — Si la réputation des scribes en matière de mathématiques est, d ordre général, inférieure à celle des Babyloniens ou des Grecs, la géométrie, au regard des prouesses techniques réalisées très tôt dans leur histoire, fut leur domaine de… … Wikipédia en Français
Géométrie projective — En mathématiques, la géométrie projective est le domaine de la géométrie qui modélise les notions intuitives de perspective et d horizon. Elle étudie les propriétés inchangées des figures par projection. Sommaire 1 Considérations historiques 2… … Wikipédia en Français
Théorème de l'angle inscrit et de l'angle au centre — Figure 1 : angles inscrits AMB = ANB et angle au centre AOB En géométrie euclidienne plane, plus précisément dans la géométrie du cercle, les théorèmes de l angle inscrit et de l angle au centre établissent des relations liant les angles… … Wikipédia en Français
Theoreme de l'angle inscrit et de l'angle au centre — Théorème de l angle inscrit et de l angle au centre Figure 1 : angles inscrits AMB = ANB et angle au centre AOB En géométrie euclidienne plane, plus précisément dans la géométrie du cercle, les théorèmes de l angle inscrit et de l angle au… … Wikipédia en Français

