- Caracterisation (mathematiques)
-
Caractérisation (mathématiques)
En jargon mathématique, l'affirmation qu'une propriété P caractérise un objet X signifie non seulement que X possède la propriété P mais de plus que X est le seul objet à posséder la propriété P. Il est également assez courant de rencontrer des affirmations telles que la propriété Q caractérise Y à un isomorphisme près. Le premier type d'affirmation dit en d'autres termes que l'ensemble des objets vérifiant la propriété P est un singleton. La seconde indique que l'ensemble de tous les objets vérifiant Q forme une simple classe d'équivalence (à la place d'isomorphisme dans l'exemple donné juste avant le mot près, une autre relation d'équivalence pourrait être spécifiée.)
Exemples
- L'exponentielle est caractérisée comme l'unique fonction réelle qui vaut 1 en 0 et qui est égale à sa dérivée.
- Parmi les lois de probabilité sur l'intervalle
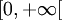de la droite réelle, sans mémoire caractérise les lois exponentielles. Cette affirmation signifie que les lois exponentielles sont les seules lois de probabilité à être sans mémoire. - Selon le théorème de Bohr-Mollerup, parmi les fonctions f telles que f(1) = 1 et
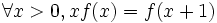, la log-convexité caractérise la fonction gamma. Cela signifie que parmi ces fonctions, la fonction gamma est la seule fonction à être log-convexe. (Une fonction f est log-convexe si par définition 
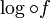est une fonction convexe. La base du logarithme n'a pas d'importance du moment où celle-ci est strictement supérieure à 1, mais par convention certains mathématiciens prennent le log sans indice pour désigner le logarithme naturel celui de base e. - Le cercle peut être caractérisé comme une variété à une dimension, compacte et connexe ; ici la caractérisation, en tant que variété lisse est à un isomorphisme près.
Portail des mathématiques
Catégorie : Vocabulaire des mathématiques
Wikimedia Foundation. 2010.
