- Près (mathématiques)
-
À quelque chose près
En mathématiques, l'expression à ... près peut avoir plusieurs sens différents.
Elle peut indiquer la précision d'une valeur approchée ou d'une approximation. Par exemple, « a est une valeur approchée de x à
près » signifie que la condition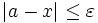 
est vérifiée.Elle peut aussi signifier que des éléments d'une certaine classe d'équivalence doivent être considérés comme ne faisant qu'un. Dans l'expression à xxx près, xxx représente alors une propriété ou un processus qui transforment un élément en un autre de la même classe d'équivalence, c'est-à-dire en un élément qui est considéré comme équivalent au premier. En théorie des groupes par exemple, nous pouvons avoir un groupe G agissant sur un ensemble X, auquel cas on peut dire que deux éléments de X sont équivalents « à l'action de groupe près », s'ils appartiennent à la même orbite.
Exemples
Dans le problème des huit reines, si les huit reines sont considérées comme distinctes, il y a 3 709 440 solutions distinctes. Cependant, les reines sont normalement considérées comme identiques, et on indique qu'il y a de 92 (= 3709440/8!) solutions uniques à une permutation près des reines, ce qui signifie que deux arrangements différents des reines sont considérés comme équivalents si l'un s'obtient à partir de l'autre par une permutation des reines; ainsi dans les deux arrangements les mêmes places sont occupées par les reines sur l'échiquier.
Si en plus de considérer les reines comme identiques, les rotations et réflections de l'échiquier sont permises, il y a seulement 12 solutions distinctes à une symétrie près, ce qui signifie que deux arrangements symétriques l'un de l'autre sont considérés comme équivalents.
Dans des contextes informels, les mathématiciens emploient souvent le mot modulo (ou en abrégé « mod. ») dans le même but, comme dans la phrase « modulo un isomorphisme, il y a deux groupes d'ordre 4 », ou « il y a 92 solutions modulo les noms des reines ». C'est une extension de la la construction « 7 et 11 sont égaux modulo 4 » utilisée en arithmétique modulaire, qui suppose que l'auditeur soit au courant d'un tel jargon mathématique.
Un autre exemple typique est l'affirmation en théorie des groupes: « il y a deux groupes d'ordre 4 à un isomorphisme près. Elle signifie qu'il y a deux classes d'équivalence de groupes d'ordre 4, et nous considérons des groupes comme identiques s'ils sont isomorphes.
Voir aussi
Portail des mathématiques
Catégorie : Vocabulaire des mathématiques
Wikimedia Foundation. 2010.
