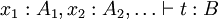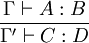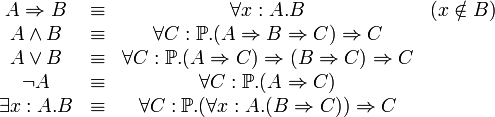Calcul des Constructions

Calcul des constructions

Le calcul des constructions (CoC de l'anglais calculus of constructions) est un lambda-calcul typé d'ordre supérieur dans lequel les types sont des valeurs de première classe. Il est par conséquent possible, dans le CoC, de définir des fonctions qui vont des entiers vers les entiers, mais aussi des entiers vers les types ou des types vers les types.

Le CoC est fortement normalisant, bien que, d'après le théorème d'incomplétude de Gödel, il soit impossible de démontrer cette propriété dans le CoC lui-même, puisqu'elle implique sa cohérence.

Le CoC a été développé initialement par Thierry Coquand.

Le CoC a été à l'origine des premières versions de l'assistant de preuves Coq. Les versions suivantes ont été construites à partir du calcul des constructions inductives qui est une extension du CoC qui intègre des types de données inductives. Dans le CoC originel, les types de données inductives devaient être émulés à l'aide de leur fonction de destruction.

Bases du calcul des constructions

Le calcul des constructions peut être considéré comme une extension de la correspondance de Curry-Howard. Cette dernière associe chaque terme du lambda-calcul simplement typé à une preuve en déduction naturelle dans la logique propositionnelle intuitionniste, et réciproquement. Le calcul des constructions étend cet isomorphisme aux preuves dans le calcul des prédicats intuitionniste dans son ensemble, ce qui inclut par conséquent des preuves de formules quantifiées (que l'on appellera également « propositions »).

Termes

Un terme du calcul des constructions est construit à l'aide des règles suivantes :

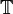$\mathbb{T}$ est un terme (également appelé Type)
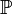$\mathbb{P}$ est un terme (également appelé Prop, le type de toutes les propositions)
Si A et B sont des termes, le sont également :
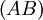
- $\mathbf{(} A B )$
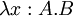- ( $\mathbf{\lambda}x:A . B$ )
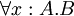- ( $\forall x:A . B$ )

Le calcul des constructions possède cinq types d'objets :

les preuves, qui sont des termes dont les types sont des propositions ;
les propositions, qui sont aussi appelées petits types ;
les prédicats, qui sont des fonctions qui retournent des propositions ;
les types larges, qui sont des types de prédicats (par exemple P est un type large) ;
T lui-même, qui est le type des types larges.

Jugements

Dans le calcul des constructions, un jugement est une inférence de typage :

$x_1:A_1, x_2:A_2, \ldots \vdash t:B$

qui peut être lue comme l'implication

si les variables 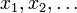$x_1, x_2, \ldots$ ont pour types 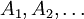$A_1, A_2, \ldots$ , alors le terme

t

a pour type

B

Les jugements valides pour le calcul des constructions sont dérivables à partir d'un ensemble de règle d'inférences. Dans la suite, on utilisera $Γ$ pour signifier une suite d'associations de type 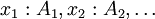$x_1:A_1, x_2:A_2, \ldots$ , et on écrira K pour désigner soit P soit T. On notera $A : B : C$ pour signifier « $A$ a pour type $B$ , et $B$ a pour type $C$ », et $B (x : = N)$ le résultat de la substitution de la variable $x$ par le terme $N$ dans le terme $B$ .

Une règle d'inférence est écrite sous la forme

${\Gamma \vdash A:B} \over {\Gamma' \vdash C:D}$

ce qui signifie

si 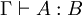$\Gamma \vdash A:B$ est un jugement valide, alors 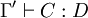$\Gamma' \vdash C:D$ l'est aussi.

Règles d'inférence du calcul des constructions

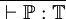
Sorte : ${{} \over {} \vdash \mathbb{P} : \mathbb{T}}$

Variable :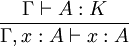 ${\Gamma \vdash A : K \over {\Gamma, x:A \vdash x : A}}$

Abstraction :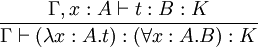 ${\Gamma, x:A \vdash t : B : K \over {\Gamma \vdash (\lambda x:A . t) : (\forall x:A . B) : K}}$

Application :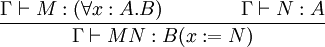 ${\Gamma \vdash M : (\forall x:A . B)\qquad\qquad\Gamma \vdash N : A \over {\Gamma \vdash M N : B(x := N)}}$

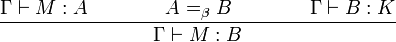
Conversion : ${\Gamma \vdash M : A \qquad \qquad A =_\beta B \qquad \qquad \Gamma\vdash B : K \over {\Gamma \vdash M : B}}$

Définir les opérateurs logique

Le calcul des constructions est très parcimonieux quand on considère uniquement ses opérateurs de base : le seul opérateur logique pour former les propositions est 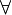$\forall$ . Néanmoins, cet opérateur unique est suffisant pour définir tous les autres opérateurs logiques :

$\begin{matrix} A \Rightarrow B & \equiv & \forall x:A . B & (x \notin B) \\ A \wedge B & \equiv & \forall C:\mathbb{P} . (A \Rightarrow B \Rightarrow C) \Rightarrow C & \\ A \vee B & \equiv & \forall C:\mathbb{P} . (A \Rightarrow C) \Rightarrow (B \Rightarrow C) \Rightarrow C & \\ \neg A & \equiv & \forall C:\mathbb{P} . (A \Rightarrow C) & \\ \exists x:A.B & \equiv & \forall C:\mathbb{P} . (\forall x:A.(B \Rightarrow C)) \Rightarrow C & \end{matrix}$

Définir des types de données

Le types de données de base utilisés en informatique peuvent être définis dans le calcul des constructions :

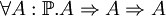
Booléens: $\forall A: \mathbb{P} . A \Rightarrow A \Rightarrow A$
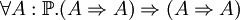
Entiers naturels: $\forall A:\mathbb{P} . (A \Rightarrow A) \Rightarrow (A \Rightarrow A)$
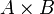
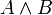
Type produit $A \times B$: $A \wedge B$
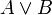
Union disjointe $A + B$: $A \vee B$

Voir aussi

Théoriciens

Thierry Coquand
Jean-Yves Girard

Références

(en) Thierry Coquand et Gerard Huet, « The Calculus of Constructions ». Information and Computation, vol. 76, n^o 2-3 (1988).
(en) Pour une source accessible librement, voir Coquand et Huet, « The calculus of constructions ». Rapport technique 530, INRIA, Centre de Rocquencourt (1986).
(en) M. W. Bunder et Jonathan P. Seldin, « Variants of the Basic Calculus of Constructions » (2004).

Portail de la logique

Ce document provient de « Calcul des constructions ».

Catégories : Logique mathématique | Théorie des types | Assistant de preuve

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Calcul des Constructions de Wikipédia en français (auteurs)

Игры ⚽ Поможем написать реферат

Regardez d'autres dictionnaires:

Calcul Des Constructions — Le calcul des constructions (CoC de l anglais calculus of constructions) est un lambda calcul typé d ordre supérieur dans lequel les types sont des valeurs de première classe. Il est par conséquent possible, dans le CoC, de définir des fonctions… … Wikipédia en Français
Calcul des constructions — Le calcul des constructions (CoC de l anglais calculus of constructions) est un lambda calcul typé d ordre supérieur dans lequel les types sont des valeurs de première classe. Il est par conséquent possible, dans le CoC, de définir des fonctions… … Wikipédia en Français
Calcul des structures et modélisation — Le calcul des structures et la modélisation concernent deux domaines distincts : d une part les applications spécifiques au patrimoine architectural, mobilier et naturel et d autre part les applications industrielles. Le calcul des… … Wikipédia en Français
CALCUL INFINITÉSIMAL - Calcul à une variable — Créée au XVIIe siècle par Newton, Leibniz et leurs prédécesseurs immédiats, transformée au XVIIIe, par Euler, en un prodigieux instrument de calcul, débarrassée, sous la Restauration, de sa métaphysique par le baron Cauchy, l’analyse… … Encyclopédie Universelle
CONSTRUCTIONS MÉTALLIQUES — Les constructions métalliques constituent un domaine important d’utilisation des produits laminés sortis de la forge. Elles emploient, en particulier, les tôles et les profilés. Les structures constituées à partir de ces éléments nécessitent des… … Encyclopédie Universelle
Calcul Du Centre De Gravité D'un Polygone — Centre de gravité d une plaque homogène En mécanique, le centre de gravité d une plaque homogène est le point par rapport auquel la masse est uniformément répartie. Pratiquement, c est le centre d équilibre de la plaque. On dit qu une plaque est… … Wikipédia en Français
Calcul du centre de gravite d'un polygone — Centre de gravité d une plaque homogène En mécanique, le centre de gravité d une plaque homogène est le point par rapport auquel la masse est uniformément répartie. Pratiquement, c est le centre d équilibre de la plaque. On dit qu une plaque est… … Wikipédia en Français
Calcul du centre de gravité d'un polygone — Centre de gravité d une plaque homogène En mécanique, le centre de gravité d une plaque homogène est le point par rapport auquel la masse est uniformément répartie. Pratiquement, c est le centre d équilibre de la plaque. On dit qu une plaque est… … Wikipédia en Français
Lambda-Calcul — « La notion de λ définissabilité fut la première de ce qui est accepté maintenant comme l équivalent exact des descriptions mathématiques pour lesquelles des algorithmes existent. » Stephen Kleene, in Origins of Recursive Function … Wikipédia en Français
Lambda-calcul — Le lambda calcul (ou λ calcul) est un système formel inventé par Alonzo Church dans les années 1930, qui fonde les concepts de fonction et d application. Il a été le premier formalisme utilisé pour définir et caractériser les fonctions récursives … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Calcul des Constructions

Calcul des constructions

Sommaire