C++0x

C++0x: C++1x

C++1x, anciennement connu sous le nom de C++0x, est la nouvelle norme prévue pour le langage C++ en informatique. Elle vise à remplacer la norme existante, ISO/IEC 14882, publiée en 1998 et mise à jour en 2003. Ces dernières sont plus connues sous le nom informel de C++98 et C++03. La nouvelle norme introduira plusieurs nouveautés au langage initial, ainsi que de nouvelles fonctionnalités à la bibliothèque standard du C++ comme la plupart des bibliothèques du "Technical Report 1", à l'exception de la bibliothèque de fonctions mathématiques spéciales. Cette norme n'étant pas à l'heure actuelle finalisée, cet article pourrait ne pas refléter l'état d'avancement courant de C++0x, qui est publié sur le site de comité de la norme ISO C++. Le rapport le plus récent, N2597, a été publié en mai 2008.

Le comité de normalisation ISO/CEI JTC1/SC22/WG21 du C++ a pour but de présenter la nouvelle norme en 2009 (par conséquent la norme appelée actuellement C++0x s'appellera C++09), ce qui signifie que le document doit être prêt pour ratification par les membres de l'ISO en 2008. Pour pouvoir finir en temps et en heure, le comité a décidé de concentrer ses efforts sur les solutions apportées jusqu'à 2006 et d'ignorer toutes les nouvelles propositions.

Un langage de programmation comme le C++ suit une évolution qui permettra aux programmeurs de coder plus rapidement, de façon plus élégante et permettant de faire du code maintenable. Ce processus soulève inévitablement des questions de compatibilité avec le code existant, ce qui s'est produit de temps en temps pendant le processus de développement du C++. Cependant, d'après l'annonce faite par Bjarne Stroustrup (l'inventeur du langage C++ et membre du comité), la nouvelle norme sera presque compatible à 100% avec la norme actuelle.

Sommaire

1 Changements prévus pour la mise à jour de la norme

2 Extensions du langage

2.1 Multitâche

2.1.1 Mémoire locale pour un thread

2.1.2 Le modificateur volatile

2.2 Les classes

2.2.1 Délégation du constructeur

2.2.2 Héritage du constructeur

2.2.3 Initialiseurs d'attributs

2.2.4 Sizeof sur les attributs de classes sans objet explicite

2.2.5 Suppression et mise à défaut des fonctions standards des objets

2.2.6 Opérateur de conversion explicite

2.2.7 Liste d'initialiseurs

2.2.8 Modification de la définition des POD (Plain Old Data)

2.3 Les Templates

2.3.1 Alias de templates grâce au mot clé using (template typedef)

2.3.2 Nombre de paramètres template infini

2.3.3 Les Concepts

2.3.4 Les chevrons (<>)

2.3.5 Template extern

2.4 Autres nouvelles fonctionnalités du C++0x

2.4.1 Expressions constantes généralisées

2.4.2 Assertions statiques

2.4.3 Expressions et fonctions lambda

2.4.4 Détermination du type

2.4.5 Sémantique des RValues Reference/Move

2.4.6 Énumérations fortement typées

2.4.7 Boucles basées sur des intervalles

2.4.8 Nouveaux littéraux "chaînes de caractères"

2.4.9 Littéraux définis par l'utilisateur

2.4.10 Destruction des objets transparentes

2.4.11 Pointeur NULL

3 Extension de la bibliothèque standard

3.1 Améliorations des threads

3.2 Le type tuple

3.3 Table de hachage

3.4 Expressions rationnelles

3.5 "Smart pointer" généraux

3.6 Amélioration des nombres aléatoires extensibles

3.7 Fonctions mathématiques spéciales

3.8 Conversion de références

3.9 Conversion polymorphe pour les objets fonctions

3.10 Type traits pour la métaprogrammation

3.11 Méthode uniforme pour calculer le type de retour des objets fonctions

4 Liens externes

Changements prévus pour la mise à jour de la norme

Comme dit précédemment, les changements du langage C++ seront situés autant dans le langage initial, que dans la bibliothèque standard.

Durant le développement de chaque fonctionnalité de la nouvelle norme, le comité a appliqué les directives suivantes :

Garder la stabilité et la compatibilité avec le C++98 et, si possible, avec le C.

Préférer l'introduction de nouvelles fonctionnalités par la bibliothèque standard, plutôt que par le langage lui-même.

Préférer les changements qui peuvent faire évoluer les techniques de programmation.

Améliorer le C++ pour faciliter la mise en place de systèmes et de bibliothèques, plutôt qu'introduire de nouvelles fonctionnalités seulement utiles pour des applications spécifiques.

Augmenter la protection des types en fournissant des alternatives plus sécurisées que les actuelles, plutôt non sécurisées.

Augmenter les performances et les capacités à travailler directement avec le matériel.

Proposer des solutions propres aux problèmes actuels.

Implémenter le principe du "zero-overhead".

Rendre le C++ facile à apprendre et à enseigner sans enlever les fonctionnalités requises par les programmeurs experts.

Extensions du langage

Multitâche

Mémoire locale pour un thread

Le modificateur volatile

Les classes

Délégation du constructeur

Héritage du constructeur

Initialiseurs d'attributs

Sizeof sur les attributs de classes sans objet explicite

Suppression et mise à défaut des fonctions standards des objets

Opérateur de conversion explicite

Liste d'initialiseurs

Modification de la définition des POD (Plain Old Data)

Les Templates

Alias de templates grâce au mot clé using (template typedef)

Nombre de paramètres template infini

Les Concepts

Les concepts ont été retirés de la prochaine norme

Les chevrons (<>)

Template extern

Autres nouvelles fonctionnalités du C++0x

Expressions constantes généralisées

Assertions statiques

La bibliothèque BOOST propose déjà cette facilité à travers la macro BOOST_STATIC_ASSERT. Cependant son implémentation est étrange, basé sur la métaprogrammation et des comparaisons de taille de structures intermédiaires créés pour l'assertion sans trop de rapport avec le concept d'assert. Par conséquent, intégrer la fonction dans le langage apporte une solution propre au problème.

En pratique, une assertion statique permet de vérifier à la compilation qu'une valeur est vraie. Par exemple, il est possible d'implémenter les concepts en utilisant boost::traits et BOOST_STATIC_ASSERT. Si une classe template nécessite que son type template soit un POD, elle peut faire une assertion statique sur boost::is_pod<T>::type::value, ce qui est un constante intégrale de type unspecified-bool-type et remplit dont le critère pour paraître dans une assertion statique.

En outre, en C++0x, l'expression

static_assert(sizeof(long) > sizeof(int))

permettrait a une bibliothèque d'être certaine qu'elle est compilée sur un système vérifiant cette condition. (x86-64 par exemple)

Expressions et fonctions lambda

Détermination du type

Le mot-clé auto se voit assigner une nouvelle sémantique par le nouveau standard. Nous connaissions son unique sémantique d'indicateur de classe de stockage pour une variable. En effet, déclarer une variable en auto revenait à indiquer au compilateur que la variable était valide seulement dans l'espace où elle était déclarée; ce comportement par défaut, le mot clé était inutile. Dans le nouveau standard, il change de sémantique et prend la place du type dans la déclaration. Le type sera alors automatiquement décidé par correspondance avec le type retourné par l'objet utilisé pour l'initialisation de la variable. exemple:

auto f = boost::bind(MyFunc, _1); f(5);

le type de f est un type interne de la bibliothèque surchargé environ quatre-vingts fois avec un script Perl. Trouver le type exact pour stocker le résultat d'un bind dans un objet n'était pas pratique du tout avant la fonctionnalité auto.

Sémantique des RValues Reference/Move

Énumérations fortement typées

Boucles basées sur des intervalles

Nouveaux littéraux "chaînes de caractères"

Littéraux définis par l'utilisateur

Destruction des objets transparentes

Pointeur NULL

Le nouveau mot-clé nullptr a été proposé comme constante du langage avec le caractère particulier d'être assignable a tous les types de pointeurs. En effet, contrairement au C où la macro préprocesseur est généralement définie comme #define NULL ((void*)0 ), en C++ il est interdit d'assigner un void* a un pointeur d'un type différent. L'usage était donc de définir NULL avec l'entier 0. Ce comportement restera compatible, mais il sera aussi possible d'écrire T* ptr = nullptr;

Extension de la bibliothèque standard

Améliorations des threads

Le type tuple

Un tuple est une collection de dimension fixe d'objets de type différents. Tous types d'objets peut être élément d'un tuple. Cette nouvelle fonctionnalité est implémentée dans un nouveau header et bénéficie des extensions de C++0x comme :

Paramètres template infini

Référence sur référence

Arguments par défaut pour les fonctions template

La définition de la classe templatée tuple est :

template <class... Types> class tuple;

Un exemple de définition et d'utilisation du type tuple :

typedef tuple< int, double, long &, const char * > test_tuple ; long lengthy = 12 ; test_tuple proof( 18, 6.5, lengthy, "Ciao!" ) ; lengthy = get<0>(proof) ; // Assigne à 'lengthy' la valeur 18. get<3>(proof) = " Beautiful!" ; // Modifie la 4ème valeur du tuple

Il est possible de créer le tuple proof sans définir son contenu si les éléments du tuple possèdent un constructeur par défaut. De plus, il est possible d'assigner un tuple à un autre tuple : si les deux tuples sont de même type, il est nécessaire que chaque élément du tuple ait un constructeur par copie, sinon il faut que le type de chaque élément de l'opérande de droite soit compatible avec le type correspondant dans l'opérande de gauche ou que l'élément correspondant de l'opérande gauche ait un constructeur approprié.

typedef tuple< int , double, string > tuple_1 t1 ; typedef tuple< char, short , const char * > tuple_2 t2( 'X', 2, "Hola!" ) ; t1 = t2 ; // Ok, les deux premiers élément peuvent être convertis // Le troisième peut être construit à partir du 'const char *'.

Les opérateurs relationnels sont disponibles (pour les tuples ayant le même nombre d'éléments). Deux expressions sont introduites pour vérifier les caractéristiques d'un tuple (à la compilation) :

tuple_size<T>::value retourne le nombre d'éléments du tuple T,

tuple_element<I, T>::type retourne le type de l'objet placé en position I du tuple T.

Table de hachage

Intégrer les tables de hachage (conteneurs associatifs non ordonnés) dans la bibliothèque standard du C++ est l'une des demandes les plus récurrentes. Cela n'avait pas été réalisé pour la norme actuelle (celle écrite en 1995 et approuvée en 1998) à cause des contraintes de temps. Bien que cette solution soit moins efficace que les arbres équilibrés dans le pire des cas (en cas de collisions importantes), elle est cependant la meilleure dans la plupart des applications réelles.

Les collisions seront uniquement gérées par chaînage linéaire car le comité ne considère pas opportun de standardiser des solutions d'adressage ouvert qui introduisent un nombre important de problèmes intrinsèques (en particulier quand la suppression d'éléments est permise). Pour éviter les conflits de noms avec les bibliothèques non standards qui ont leur propre implémentation des tables de hachage, on utilisera le préfixe unordered, au lieu de hash.

Cette nouvelle fonctionnalité intégrera quatre types de tables de hachage, différentes selon qu'elles acceptent ou non des éléments de même clé (clé unique ou clé équivalente) et qu'elles associent chaque clé à la valeur associée.

Type de table de hachage Type associé arbitraire Clés équivalentes

unordered_set

unordered_multiset •

unordered_map •

unordered_multimap • •

Ces nouvelles classes remplissent toutes les demandes des classes de conteneurs et contiennent toutes les méthodes nécessaires pour accéder aux éléments : insert, erase, begin, end.

Ces classes n'ont pas nécessité les nouvelles extensions du langage C++ mais seulement une légère extension du header <functional> et l'introduction des headers <unordered_set> et <unordered_map>. Aucun autre changement aux classes de la norme actuelle n'est nécessaire et elles ne dépendent d'aucune autre extension de la bibliothèque standard.

Expressions rationnelles

"Smart pointer" généraux

Amélioration des nombres aléatoires extensibles

Fonctions mathématiques spéciales

Le fichier header <math> définit déjà plusieurs fonctions mathématiques usuelles:

trigonométriques: sin, cos, tan, asin, acos, atan, atan2;

hyperboliques: sinh, cosh, tanh, asinh, acosh, atanh;

exponentielles: exp, exp2, frexp, ldexp, expm1;

logarithmiques: log10, log2, logb, ilogb, log1p;

puissances: pow, sqrt, cbrt, hypot;

spéciales: erf, erfc, tgamma, lgamma.

Le comité a décidé d'ajouter de nouvelles fonctions qui nécessitent actuellement l'utilisation de bibliothèques non-standards. Ces nouvelles fonctions auront un intérêt principalement pour les programmeurs de disciplines scientifique et pour l'ingénierie.

Le tableau suivant montre les 23 fonctions décrites dans TR1.

Nom de la fonction Prototype de la fonction Expression mathématique

Polynômes de Laguerre généralisés double assoc_laguerre( unsigned n, unsigned m, double x ) ; 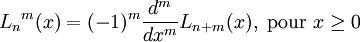${L_n}^m(x) = (-1)^m \frac{d^m}{dx^m} L_{n+m}(x), \text{ pour } x \ge 0$

Polynômes de Legendre généralisés double assoc_legendre( unsigned l, unsigned m, double x ) ; 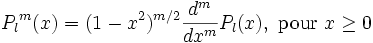${P_l}^m(x) = (1-x^2)^{m/2} \frac{d^m}{dx^m} P_l(x), \text{ pour } x \ge 0$

Fonction Beta double beta( double x, double y ) ; 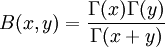$B(x,y)=\frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)}$

Intégrale elliptique complète de premier genre double comp_ellint_1( double k ) ; 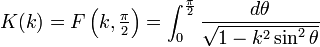$K(k) = F\left(k, \textstyle \frac{\pi}{2}\right) = \int_0^{\frac{\pi}{2}} \frac{d\theta}{\sqrt{1 - k^2 \sin^2 \theta}}$

Intégrale elliptique complète de deuxième genre double comp_ellint_2( double k ) ; 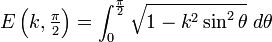$E\left(k, \textstyle \frac{\pi}{2}\right) = \int_0^{\frac{\pi}{2}} \sqrt{1 - k^2 \sin^2 \theta}\; d\theta$

Intégrale elliptique complète de troisième genre double comp_ellint_3( double k , double nu ) ; 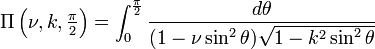$\Pi\left(\nu, k, \textstyle \frac{\pi}{2}\right) = \int_0^{\frac{\pi}{2}} \frac{d\theta}{(1 - \nu \sin^2 \theta)\sqrt{1 - k^2 \sin^2 \theta}}$

Fonctions hypergéométriques confluentes double conf_hyperg( double a, double c, double x ) ; 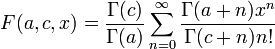$F(a, c, x) = \frac{\Gamma(c)}{\Gamma(a)} \sum_{n = 0}^\infty \frac{\Gamma(a + n) x^n}{\Gamma(c + n) n!}$

Fonctions de Bessel cylindriques modifiées régulières double cyl_bessel_i( double nu, double x ) ; 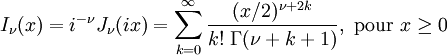$I_\nu(x) = i^{-\nu} J_\nu(ix) = \sum_{k = 0}^\infty \frac{(x/2)^{\nu + 2k}}{k! \; \Gamma(\nu + k + 1)}, \text{ pour } x \ge 0$

Fonctions de Bessel cylindriques du premier genre double cyl_bessel_j( double nu, double x ) ; 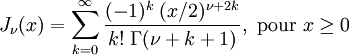$J_\nu(x) = \sum_{k = 0}^\infty \frac{(-1)^k \; (x/2)^{\nu + 2k}}{k! \; \Gamma(\nu + k + 1)}, \text{ pour } x \ge 0$

Fonctions de Bessel cylindriques modifiées irrégulières double cyl_bessel_k( double nu, double x ) ; $\begin{align} K_\nu(x) & = \textstyle\frac{\pi}{2} i^{\nu+1} \big(J_\nu(ix) + i N_\nu(ix)\big) \\ & = \begin{cases} \displaystyle \frac{I_{-\nu}(x) - I_\nu(x)}{\sin \nu\pi}, & \text{ pour } x \ge 0 \text{ et } \nu \notin \mathbb{Z} \\[10pt] \displaystyle \frac{\pi}{2} \lim_{\mu \to \nu} \frac{I_{-\mu}(x) - I_\mu(x)}{\sin \mu\pi}, & \text{ pour } x < 0 \text{ et } \nu \in \mathbb{Z} \\ \end{cases} \end{align}$

Fonctions de Neumann cylindriques
Fonctions de Bessel cylindriques du deuxième genre
double cyl_neumann( double nu, double x ) ; $N_\nu(x) = \begin{cases} \displaystyle \frac{J_\nu(x)\cos \nu\pi - J_{-\nu}(x)}{\sin \nu\pi}, & \text{ pour } x \ge 0 \text{ et } \nu \notin \mathbb{Z} \\[10pt] \displaystyle \lim_{\mu \to \nu} \frac{J_\mu(x)\cos \mu\pi - J_{-\mu}(x)}{\sin \mu\pi}, & \text{ pour } x < 0 \text{ et } \nu \in \mathbb{Z} \\ \end{cases}$

Intégrale elliptique incomplète du premier genre double ellint_1( double k, double phi ) ; 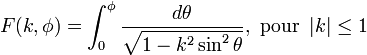$F(k,\phi)=\int_0^\phi\frac{d\theta}{\sqrt{1-k^2\sin^2\theta}}, \text{ pour } \left|k\right| \le 1$

Intégrale elliptique incomplète du deuxième genre double ellint_2( double k, double phi ) ; 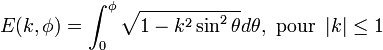$\displaystyle E(k,\phi)=\int_0^\phi\sqrt{1-k^2\sin^2\theta}d\theta, \text{ pour } \left|k\right| \le 1$

Intégrale elliptique incomplète du troisième genre double ellint_3( double k, double nu, double phi ) ; 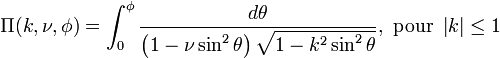$\Pi(k,\nu,\phi)=\int_0^\phi\frac{d\theta}{\left(1-\nu\sin^2\theta\right)\sqrt{1-k^2\sin^2\theta}}, \text{ pour } \left|k\right| \le 1$

Intégrale exponentielle double expint( double x ) ; 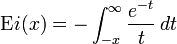$\mbox{E}i(x)=-\int_{-x}^{\infty} \frac{e^{-t}}{t}\, dt$

Polynômes d'Hermite double hermite( unsigned n, double x ) ; 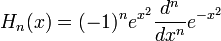$H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}e^{-x^2}\,\!$

Séries hypergeometriques double hyperg( double a, double b, double c, double x ) ; 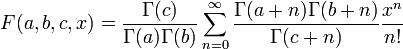$F(a,b,c,x)=\frac{\Gamma(c)}{\Gamma(a)\Gamma(b)}\sum_{n = 0}^\infty\frac{\Gamma(a+n)\Gamma(b+n)}{\Gamma(c+n)}\frac{x^n}{n!}$

Polynômes de Laguerre double laguerre( unsigned n, double x ) ; 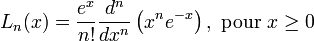$L_n(x)=\frac{e^x}{n!}\frac{d^n}{dx^n}\left(x^n e^{-x}\right), \text{ pour } x \ge 0$

Polynômes de Legendre double legendre( unsigned l, double x ) ; 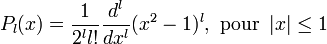$P_l(x) = {1 \over 2^l l!} {d^l \over dx^l } (x^2 -1)^l, \text{ pour } \left|x\right| \le 1$

Fonction zeta de Riemann double riemann_zeta( double x ) ; $\Zeta(x) = \begin{cases} \displaystyle \sum_{k = 1}^\infty k^{-x}, & \text{ pour } x > 1 \\[10pt] \displaystyle 2^x\pi^{x-1}\sin\left(\frac{x\pi}{2}\right)\Gamma(1-x)\zeta(1-x), & \text{ pour } x < 1 \\ \end{cases}$

Fonctions sphériques de Bessel du premier genre double sph_bessel( unsigned n, double x ) ; 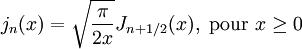$j_n(x) = \sqrt{\frac{\pi}{2x}} J_{n+1/2}(x), \text{ pour } x \ge 0$

Fonctions sphériques de Legendre généralisées double sph_legendre( unsigned l, unsigned m, double theta ) ; $Y_{l}^{m}(\theta, 0) \text{ avec } Y_{l}^{m}(\theta, \phi) = (-1)^{m}\left[\frac{(2l+1)}{4\pi}\frac{(l-m)!}{(l+m)!}\right]^{1 \over 2} P_{l}^{m}(cos \theta)e^{im\phi} \text{ pour } |m| \leq l$

Fonctions sphériques de Neumann
Fonctions sphériques de Bessel du deuxième genre
double sph_neumann( unsigned n, double x ) ; 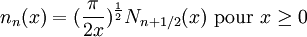$n_{n}(x) = (\frac{\pi}{2x} )^{1 \over 2} N_{n+1/2}(x) \text{ pour } x \geq 0$

Chacune de ces fonctions possède deux variantes supplémentaires. En rajoutant le suffixe ‘f’ ou ‘l’ au nom de la fonction, on obtient les mêmes fonctions agissant sur des float ou des long double respectivement. Par exemple :

float sph_neumannf( unsigned n, float x ) ; long double sph_neumannl( unsigned n, long double x ) ;

Conversion de références

Conversion polymorphe pour les objets fonctions

Type traits pour la métaprogrammation

Méthode uniforme pour calculer le type de retour des objets fonctions

Liens externes

Le Comité du Standard C++

Page personnelle de Bjarne Stroustrup

C++0X: Le nouveau visage du Standard C++

Le blog de Herb Sutter sur le C++0x

Une interview sur le C++0x donné par Bjarne Stroustrup à l'Université de Waterloo

Une introduction rapide au C++0x (Novembre 2007)

Portail de l’informatique

Ce document provient de « C%2B%2B1x ».

Catégories : Langage de programmation | Langage orienté objet | Norme ISO | C++

Type de table de hachage	Type associé arbitraire	Clés équivalentes
unordered_set
unordered_multiset		•
unordered_map	•
unordered_multimap	•	•

Nom de la fonction	Prototype de la fonction	Expression mathématique
Polynômes de Laguerre généralisés	double assoc_laguerre( unsigned n, unsigned m, double x ) ;	${L_n}^m(x) = (-1)^m \frac{d^m}{dx^m} L_{n+m}(x), \text{ pour } x \ge 0$
Polynômes de Legendre généralisés	double assoc_legendre( unsigned l, unsigned m, double x ) ;	${P_l}^m(x) = (1-x^2)^{m/2} \frac{d^m}{dx^m} P_l(x), \text{ pour } x \ge 0$
Fonction Beta	double beta( double x, double y ) ;	$B(x,y)=\frac{\Gamma(x) \Gamma(y)}{\Gamma(x+y)}$
Intégrale elliptique complète de premier genre	double comp_ellint_1( double k ) ;	$K(k) = F\left(k, \textstyle \frac{\pi}{2}\right) = \int_0^{\frac{\pi}{2}} \frac{d\theta}{\sqrt{1 - k^2 \sin^2 \theta}}$
Intégrale elliptique complète de deuxième genre	double comp_ellint_2( double k ) ;	$E\left(k, \textstyle \frac{\pi}{2}\right) = \int_0^{\frac{\pi}{2}} \sqrt{1 - k^2 \sin^2 \theta}\; d\theta$
Intégrale elliptique complète de troisième genre	double comp_ellint_3( double k , double nu ) ;	$\Pi\left(\nu, k, \textstyle \frac{\pi}{2}\right) = \int_0^{\frac{\pi}{2}} \frac{d\theta}{(1 - \nu \sin^2 \theta)\sqrt{1 - k^2 \sin^2 \theta}}$
Fonctions hypergéométriques confluentes	double conf_hyperg( double a, double c, double x ) ;	$F(a, c, x) = \frac{\Gamma(c)}{\Gamma(a)} \sum_{n = 0}^\infty \frac{\Gamma(a + n) x^n}{\Gamma(c + n) n!}$
Fonctions de Bessel cylindriques modifiées régulières	double cyl_bessel_i( double nu, double x ) ;	$I_\nu(x) = i^{-\nu} J_\nu(ix) = \sum_{k = 0}^\infty \frac{(x/2)^{\nu + 2k}}{k! \; \Gamma(\nu + k + 1)}, \text{ pour } x \ge 0$
Fonctions de Bessel cylindriques du premier genre	double cyl_bessel_j( double nu, double x ) ;	$J_\nu(x) = \sum_{k = 0}^\infty \frac{(-1)^k \; (x/2)^{\nu + 2k}}{k! \; \Gamma(\nu + k + 1)}, \text{ pour } x \ge 0$
Fonctions de Bessel cylindriques modifiées irrégulières	double cyl_bessel_k( double nu, double x ) ;	$\begin{align} K_\nu(x) & = \textstyle\frac{\pi}{2} i^{\nu+1} \big(J_\nu(ix) + i N_\nu(ix)\big) \\ & = \begin{cases} \displaystyle \frac{I_{-\nu}(x) - I_\nu(x)}{\sin \nu\pi}, & \text{ pour } x \ge 0 \text{ et } \nu \notin \mathbb{Z} \\[10pt] \displaystyle \frac{\pi}{2} \lim_{\mu \to \nu} \frac{I_{-\mu}(x) - I_\mu(x)}{\sin \mu\pi}, & \text{ pour } x < 0 \text{ et } \nu \in \mathbb{Z} \\ \end{cases} \end{align}$
Fonctions de Neumann cylindriques Fonctions de Bessel cylindriques du deuxième genre	double cyl_neumann( double nu, double x ) ;	$N_\nu(x) = \begin{cases} \displaystyle \frac{J_\nu(x)\cos \nu\pi - J_{-\nu}(x)}{\sin \nu\pi}, & \text{ pour } x \ge 0 \text{ et } \nu \notin \mathbb{Z} \\[10pt] \displaystyle \lim_{\mu \to \nu} \frac{J_\mu(x)\cos \mu\pi - J_{-\mu}(x)}{\sin \mu\pi}, & \text{ pour } x < 0 \text{ et } \nu \in \mathbb{Z} \\ \end{cases}$
Intégrale elliptique incomplète du premier genre	double ellint_1( double k, double phi ) ;	$F(k,\phi)=\int_0^\phi\frac{d\theta}{\sqrt{1-k^2\sin^2\theta}}, \text{ pour } \left\|k\right\| \le 1$
Intégrale elliptique incomplète du deuxième genre	double ellint_2( double k, double phi ) ;	$\displaystyle E(k,\phi)=\int_0^\phi\sqrt{1-k^2\sin^2\theta}d\theta, \text{ pour } \left\|k\right\| \le 1$
Intégrale elliptique incomplète du troisième genre	double ellint_3( double k, double nu, double phi ) ;	$\Pi(k,\nu,\phi)=\int_0^\phi\frac{d\theta}{\left(1-\nu\sin^2\theta\right)\sqrt{1-k^2\sin^2\theta}}, \text{ pour } \left\|k\right\| \le 1$
Intégrale exponentielle	double expint( double x ) ;	$\mbox{E}i(x)=-\int_{-x}^{\infty} \frac{e^{-t}}{t}\, dt$
Polynômes d'Hermite	double hermite( unsigned n, double x ) ;	$H_n(x)=(-1)^n e^{x^2}\frac{d^n}{dx^n}e^{-x^2}\,\!$
Séries hypergeometriques	double hyperg( double a, double b, double c, double x ) ;	$F(a,b,c,x)=\frac{\Gamma(c)}{\Gamma(a)\Gamma(b)}\sum_{n = 0}^\infty\frac{\Gamma(a+n)\Gamma(b+n)}{\Gamma(c+n)}\frac{x^n}{n!}$
Polynômes de Laguerre	double laguerre( unsigned n, double x ) ;	$L_n(x)=\frac{e^x}{n!}\frac{d^n}{dx^n}\left(x^n e^{-x}\right), \text{ pour } x \ge 0$
Polynômes de Legendre	double legendre( unsigned l, double x ) ;	$P_l(x) = {1 \over 2^l l!} {d^l \over dx^l } (x^2 -1)^l, \text{ pour } \left\|x\right\| \le 1$
Fonction zeta de Riemann	double riemann_zeta( double x ) ;	$\Zeta(x) = \begin{cases} \displaystyle \sum_{k = 1}^\infty k^{-x}, & \text{ pour } x > 1 \\[10pt] \displaystyle 2^x\pi^{x-1}\sin\left(\frac{x\pi}{2}\right)\Gamma(1-x)\zeta(1-x), & \text{ pour } x < 1 \\ \end{cases}$
Fonctions sphériques de Bessel du premier genre	double sph_bessel( unsigned n, double x ) ;	$j_n(x) = \sqrt{\frac{\pi}{2x}} J_{n+1/2}(x), \text{ pour } x \ge 0$
Fonctions sphériques de Legendre généralisées	double sph_legendre( unsigned l, unsigned m, double theta ) ;	$Y_{l}^{m}(\theta, 0) \text{ avec } Y_{l}^{m}(\theta, \phi) = (-1)^{m}\left[\frac{(2l+1)}{4\pi}\frac{(l-m)!}{(l+m)!}\right]^{1 \over 2} P_{l}^{m}(cos \theta)e^{im\phi} \text{ pour } \|m\| \leq l$
Fonctions sphériques de Neumann Fonctions sphériques de Bessel du deuxième genre	double sph_neumann( unsigned n, double x ) ;	$n_{n}(x) = (\frac{\pi}{2x} )^{1 \over 2} N_{n+1/2}(x) \text{ pour } x \geq 0$