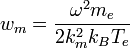- Bremsstrahlung
-
Rayonnement continu de freinage
Le rayonnement continu de freinage ou Bremsstrahlung (aussi appelé free-free emission en anglais) est un rayonnement électromagnétique à spectre large créé par le ralentissement de charges électriques. On parle aussi de rayonnement blanc.
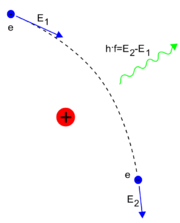
Lorsqu'une cible solide est bombardée par un faisceau d'électrons, ceux-ci sont freinés et déviés par le champ électrique des noyaux de la cible. Or, selon les équations de Maxwell, toute charge dont la vitesse varie, en valeur absolue ou en direction, rayonne. Comme la décélération des électrons n'est pas quantifiée, cela crée un flux de photons dont le spectre en énergie est continu.
Sommaire
Applications
Ce procédé est notamment utilisé pour produire des rayons X, dans les générateurs de rayons X et les synchrotrons. Ces deux sources ne donnent pas le même type de spectre. En effet, le rayonnement synchrotron est purement continu, contrairement à celui d'un tube à rayons X, qui comporte quelques raies spectrales, dû à des transitions électroniques.
Forme du spectre
L'énergie maximale des photons est l'énergie cinétique initiale E0 des électrons. Le spectre en énergie s'arrête donc à cette valeur E0. Si l'on trace le spectre en longueur d'onde (représentation la plus fréquente), on a un spectre qui commence à λ0 qui vaut
ou encore
et dont l'énergie est maximale pour λmax qui vaut
où
- h est la constante de Planck ;
- c est la vitesse de la lumière dans le vide ;
- e est la charge électrique élémentaire de l'électron ;
- U est la tension appliquée au tube à rayons X.
Bremsstrahlung thermique
Dans un plasma, les électrons libres produisent constamment un Bremsstrahlung lorsqu'ils entrent en collision avec des ions. Dans un plasma uniforme contenant des électrons thermiques[note 1], la densité spectrale de puissance[note 2] du Bremsstrahlung émis se calcule à partir de l'équation différentielle[1] :
où ne est la densité de nombre des électrons, re est le rayon classique de l'électron, me est la masse de l'électron, kB est la constante de Boltzmann et c est la vitesse de la lumière dans le vide. Les deux premiers facteurs entre crochets à la droite de l'égalité sont sans dimension. L'état de la charge « efficace » d'un ion, Zeff, est une moyenne de la charge de tous les ions :
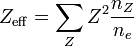 ,
,où nZ est le nombre de densité des ions portant une charge de Z. La fonction E1 est une exponentielle intégrale. La fonction wm se calcule selon :
avec km le nombre d'onde maximum ou de coupure. km = K / λB quand kBTe > 27,2Z2eV (pour une seule espèce d'ions ; 27,2 eV est le double de l'énergie d'ionisation de l'hydrogène) où K est un nombre pur et
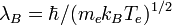 est la longueur d'onde de De Broglie. Sinon,
est la longueur d'onde de De Broglie. Sinon, 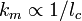 où lc est la distance classique de Coulomb selon la trajectoire la plus proche.
où lc est la distance classique de Coulomb selon la trajectoire la plus proche.dPBr / dω est infini à ω = 0 et décroît rapidement selon ω. Dans certains cas précis, il est possible de calculer analytiquement la primitive de l'équation différentielle.
Pour le cas km = K / λB, nous avons
![w_m = {1 \over 2K^2} \left[\frac{\hbar\omega}{k_B T_e}\right]^2](/pictures/frwiki/50/2a039a027e86cf6669b942f5f19cb913.png) .
.
Dans ce cas, la densité de puissance, intégrée sur toutes les fréquences, est finie et vaut
![P_\mathrm{Br} = {8 \over 3} \left[ n_er_e^3 \right]^2
\left[ {k_B T_e \over m_ec^2} \right]^{1/2}
\left[ {m_ec^3 \over r_e^4} \right] Z_\mathrm{eff} \alpha K](/pictures/frwiki/102/f473e78f51ed83f25f0c36cc15dbe193.png) .
.
La constante de structure fine α apparaît dû à la nature quantique de λB. En pratique, une version couramment utilisée de cette formule est[2] :
![P_\mathrm{Br} [\textrm{W/m}^3] = \left[{n_e \over 7.69 \times 10^{18} \textrm{m}^{-3} }\right]^2 T_e[\textrm{eV}]^{1/2} Z_\mathrm{eff}](/pictures/frwiki/57/98957303ee0f1876df3c238ccaf95ca3.png) .
.
Cette formule est proche de la valeur théorique si K=3,17 ; la valeur K=3 est suggérée par Ichimaru[1].
Pour des températures très élevées, il faut apporter des corrections relativistes en ajoutant des termes d'orde kBTe/mec2 [3].
Si le plasma est optiquement mince, la radiation du Bremsstrahlung quitte le plasma, emportant une partie de son énergie. Cet effet est appelé « refroidissement par Bremsstrahlung ».
Annexes
Références
Notes
- ↑ L'énergie des électrons suit une distribution de Maxwell-Boltzmann à une température Te.
- ↑ C'est une puissance par intervalle de fréquence angulaire par volume, intégrée sur l'angle solide en entier.
Voir aussi
Articles connexes
- Portail de la physique
Catégories : Spectre électromagnétique | Rayons X
Wikimedia Foundation. 2010.

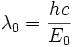
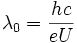
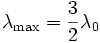
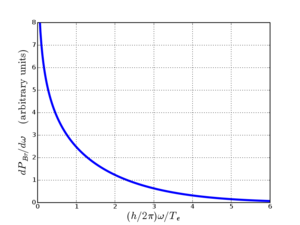
 ). Ce tracé est valide pour le cas quantique
). Ce tracé est valide pour le cas quantique ![{dP_\mathrm{Br} \over d\omega} = {4\sqrt 2 \over 3\sqrt\pi} \left[ n_er_e^3 \right]^2
\left[ { \frac{m_ec^2}{k_B T_e} } \right]^{1/2}
\left[ {m_ec^2 \over r_e^3} \right] Z_\mathrm{eff} E_1(w_m) ,](/pictures/frwiki/55/72b7a129b7cdd7ae9496db7f5e9d095f.png)