Boule (mathématiques)

Pour les articles homonymes, voir Boule.

En topologie, une boule est un type de voisinage particulier dans un espace métrique. Le nom évoque, à juste titre la boule solide dans l'espace usuel à trois dimensions, mais la notion se généralise entre autres à des espaces de dimension plus grande (ou plus petite) ou encore de norme non euclidienne. Dans ce cas, une boule peut ne pas être ronde au sens usuel du terme.

Définition générale

Dans l'espace usuel comme dans n'importe quel espace métrique, la boule fermée centrée en un point P et de rayon réel strictement positif r est l'ensemble des points dont la distance à P est inférieure ou égale à r. La boule ouverte correspondante est l'ensemble des points dont la distance à P est inférieure strictement à r.

Dans un espace vectoriel normé, la boule unité (ouverte ou fermée) est la boule centrée à l'origine et de rayon 1.

Les boules fermées des espaces euclidiens sont aussi appelés des disques.

Propriétés

• Une boule ouverte est toujours un ouvert de l'espace dans laquelle elle est définie. De même, une boule fermée est toujours un fermé.
• Dans un espace vectoriel normé, toutes les boules ouvertes (resp. fermées) sont semblables par translation et homothétie. La boule unité est toujours un convexe borné, symétrique par rapport à l'origine et d'intérieur non vide.
• Dans un espace vectoriel réel normé, la boule ouverte est l'intérieur de la boule fermée correspondante. Cela peut être faux dans d'autres espaces métriques.
• Dans un espace vectoriel réel normé de dimension finie, la boule fermée est l'adhérence de la boule ouverte. Cela peut être faux même dans certains espaces vectoriels réels.
• Une partie d'un espace topologique est ouverte si et seulement si elle est la réunion des boules qu'elle contient.

Exemples de boules exotiques

• Dans l'espace réel à trois dimensions muni de la norme infini, les boules ont une forme cubique avec des faces parallèles aux axes.
• Dans l'ensemble des entiers muni de la distance usuelle (valeur absolue de la différence), une boule ouverte de rayon 1 ne contient que son centre ; c'est donc un fermé. Inversément, la boule fermée de rayon 1 contient trois points (le centre et les deux entiers adjacents) et c'est un ouvert^[1].

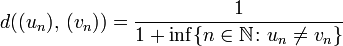Exemple de distance ultramétrique sur l'ensemble des suites d'entiers

• Dans un espace muni d'une distance ultramétrique, les boules sont à la fois ouvertes et fermées, tout point d'une boule en est un centre et si deux boules se rencontrent, l'une est contenue dans l'autre. De tels espaces se rencontrent en analyse p-adique mais aussi dans des situations plus élémentaires : sur l'ensemble des suites d'entiers, il suffit de définir la distance entre deux suites par l'inverse du plus petit rang où les termes diffèrent.

Utilisation

• Une partie d'un espace métrique est ouverte si et seulement si elle est la réunion des boules qu'elle contient.
• Le théorème de Riesz énonce qu'un espace vectoriel réel normé est de dimension fini si et seulement si sa boule fermée unité est compacte.

Notes et références

• Portail des mathématiques