Volume d'une sphère

Volume d'une sphère

Le volume d'une sphère est une mesure de l'espace délimité par une sphère.

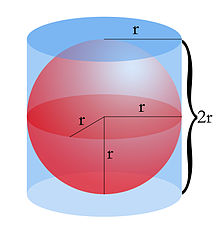
Si le rayon d'une sphère est R, son volume est 4⁄3×π×R3.

Sommaire

Histoire

Sphère inscrite dans un cylindre.

Euclide, dans la proposition 18 du livre XII de ses Éléments, vers 300 av. J-C., énonce que le volume d'une sphère est proportionnel au cube de son diamètre. Il démontre ce résultat par la méthode d'exhaustion, en encadrant la sphère par des polyèdres.

Archimède, dans De la sphère et du cylindre (vers 220 av J.-C.) compare les volumes d'une sphère, d'un cylindre et d'un cône. Il connaît le volume du cylindre et du cône et démontre que, si une sphère est inscrite dans un cylindre, alors le volume de cette sphère est égal aux deux tiers de celui du cylindre circonscrit. Il démontre que le rapport entre les aires de la sphère et du cylindre est le même qu'entre leurs volumes ; ce qu'il énonce ainsi[1] :

« Un cylindre qui a une base égale à un grand cercle d'une sphère, et une hauteur égale au diamètre de cette sphère, est égal à trois fois la moitié de cette sphère, et la surface de ce cylindre est aussi égale à trois fois la moitié de la surface de cette même sphère. »

Cette découverte fera de lui un mathématicien particulièrement important dans l'Histoire [2]. Il en est si fier qu'il donne des instructions pour que sa tombe soit gravée d'une sphère inscrite dans un cylindre[2].

Démonstrations

Par la méthode d'exhaustion

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

Par le calcul intégral

Calotasegmento esferico.png

La méthode d'Archimède (redécouverte dans le palimpseste portant son nom) consiste à découper la sphère en disques minces dont on ajoute le volume (assimilé au produit de leur surface par leur épaisseur). En langage moderne, cela revient à calculer la limite d'une somme de Riemann, et donc à calculer une intégrale définie. Si l'on considère la variable h allant de -R à R, le disque correspondant à la hauteur h a pour rayon r(h) vérifiant, d'après le théorème de Pythagore r(h)2+h2=R2 ; comme le volume de ce disque est πr(h)2dh, on obtient comme volume de la sphère \int_{-R}^R\pi(R^2-h^2)dh=4\pi R^3/3.

Notes et références

Liens internes

Sources

Notes

  1. ↑ Traduction par F. Peyrard, 1807 lire en ligne.
  2. ↑ a et b Archimedes, Britannica.

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Volume d'une sphère de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

  • Dipole magnetique d'une sphere — Dipôle magnétique d une sphère Soit une sphère, de centre O, de rayon R, parcourue par un courant de surface , de moment dipolaire , avec V volume de la boule. Plus précisément : Sommaire …   Wikipédia en Français

  • Dipole magnétique d'une sphère — Dipôle magnétique d une sphère Soit une sphère, de centre O, de rayon R, parcourue par un courant de surface , de moment dipolaire , avec V volume de la boule. Plus précisément : Sommaire …   Wikipédia en Français

  • Dipôle Magnétique D'une Sphère — Soit une sphère, de centre O, de rayon R, parcourue par un courant de surface , de moment dipolaire , avec V volume de la boule. Plus précisément : Sommaire …   Wikipédia en Français

  • Dipôle magnétique d'une sphère — Soit une sphère, de centre O, de rayon R, parcourue par un courant de surface , de moment dipolaire , avec V volume de la boule. Plus précisément : Sommaire …   Wikipédia en Français

  • SPHÈRE — n. f. T. de Géométrie Solide limité par une surface courbe dont tous les points sont à égale distance d’un point intérieur appelé Centre. Les propriétés de la sphère. Le centre, le diamètre, la circonférence de la sphère. La surface, le volume… …   Dictionnaire de l'Academie Francaise, 8eme edition (1935)

  • Sphere — Sphère Pour les articles homonymes, voir Sphère (homonymie). Une sphère dans un espace euclidien En géométrie euclidienne, une sphère es …   Wikipédia en Français

  • sphère — [ sfɛr ] n. f. • 1509; espere mil. XIIe; d ab. t. d astron.; lat. sphæra, gr. sphaira 1 ♦ Surface fermée dont tous les points sont situés à égale distance d un point donné; solide délimité par cette surface (⇒ 1. balle, 1. bille, boule). Centre,… …   Encyclopédie Universelle

  • volume — [ vɔlym ] n. m. • XIIIe; lat. volumen « feuilles manuscrites enroulées », rad. volvere « rouler » I ♦ 1 ♦ (1270) Réunion d un certain nombre de cahiers (notamment imprimés) brochés ou reliés ensemble. ⇒ 1. livre. La bibliothèque royale « s… …   Encyclopédie Universelle

  • Volume de solides usuels — Volume Pour les articles homonymes, voir Volume (homonymie). En physique, le volume d un objet mesure « l extension dans l espace » qu il possède dans les trois directions en même temps, de même que l aire d une figure dans le plan… …   Wikipédia en Français

  • Sphère — Pour les articles homonymes, voir Sphère (homonymie). Une sphère dans un espace euclidien …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”