Théorie des bifurcations

La théorie des bifurcations, en mathématiques et en physique est l'étude des systèmes dynamiques. Une bifurcation intervient lorsqu'un petit changement d'un paramètre physique produit un changement majeur dans l'organisation du système.

Exemple

L'exemple classique d'une bifurcation est celui du flambage d'une poutre élastique (l'expérience peut être faite avec une règle d'écolier). Si on compresse la poutre légèrement, elle va rester droite. Tout à coup, au delà d'une limite bien définie, la poutre va se plier se plus en plus lorsqu'on augmente la force exercée. Il y a donc bifurcation, ou brisure de symétrie, où l'on passe de l'état "poutre droite" à l'état "poutre courbée". Avant la bifurcation, l'état "poutre droite" était stable, après la bifurcation, il devient instable.

Un autre exemple canonique est la température de Curie. Au delà d'une certaine température, un matériau perd son aimantation spontanée.

Définition

Soit un système d'équations différentielles :

λ est ici le paramètre contrôlant la bifurcation (la force exercée dans l'exemple précédent). On dit qu'il y a bifurcation en λ₀ si, en une valeur de λ arbitrairement proche de λ₀, il existe une dynamique topologiquement non-équivalente à celle en λ₀.

Types de bifurcation

La théorie des bifurcations consiste à classer les différents types de bifurcation en classes. Chaque classe correspond à une certaine symétrie dans le problème. Parmi les différents types de bifurcations, on trouve :

• Les bifurcations "pitchfork". Un équilibre stable se déstabilise en un équilibre instable, et deux équilibres stables sont créés. Cette transition peut se faire de façon supercritique (de façon continue et prévisible) ou sous-critique (discontinue, avec des phénomènes d'hystérèse)
• Les bifurcations "saddle-node". Deux points d'équilibres existent (un stable et un instable) avant la bifurcation. Après la bifurcation, plus aucun équilibre n'existe.
• Les bifurcations de Hopf. Ce sont des bifurcations oscillantes, comme l'attracteur de Lorenz.
• Les bifurcations de doublement de période. Ce sont des bifurcations qui mènent à des comportements chaotiques. Elles peuvent par exemple s'obtenir en faisant rebondir une balle de ping-pong sur une surface oscillante, et en augmentant la fréquence d'oscillation.

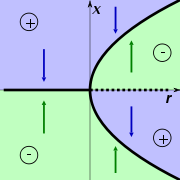
Chacune de ces bifurcations est caractérisée par une forme normale, qui est l'équation générale typique de ce type de bifurcation. Par exemple, la forme normale d'une bifurcation pitchfork supercritique est :

Bifurcation supercritique, les lignes pleines représentent des équilibres stables, les lignes en pointillés les équilibres instables.

Pour des valeurs négatives de r, x=0 est la seule solution. Pour r>0, il y a deux solutions stables .

Voir aussi

• Système dynamique/Théorie des systèmes dynamiques
• Théorie du chaos

Liens externes

http://www.scholarpedia.org/article/Bifurcation http://www.biologie.ens.fr/eceem/Berder_2010/documents/Lobry.pdf

• Portail de l'analyse
• Portail sur les sciences
• Portail de la physique