Théorie constructale

Construction d'un système constructal de refroidissement

La théorie constructale d'optimisation globale sous des contraintes locales, créée par Adrian Bejan, explique de manière simple l'émergence de nombreuses formes naturelles, en particulier des structures arborescentes, telles que les fentes de dessiccation, les méandres de rivières, les poumons, les arbres... L'idée constructale est que les architectures de flux naissent d'un principe de maximisation de l'accès aux flux, dans le temps, composée avec leur capacité à se transformer.

Cette théorie permet de concevoir des systèmes optimisés en répartissant au mieux les inévitables résistances internes du système conçu, par exemple un système de refroidissement par fluide caloriporteur, un réseau de distribution d'eau, etc.

Historique

La théorie constructale a été créée à la fin des années 90 par Adrian Bejan, diplômé du Massachusetts Institute of Technology (MIT) en 1975 (doctorat de Mécanique).

Le professeur Bejan a enseigné au MIT depuis 1976 et est actuellement professeur de Mécanique à l'Université de Duke.

Les recherches de Bejan couvrent notamment les domaines suivants: minimisation de la génération d'entropie, analyse exergétique, condensation, convection en milieu poreux, transition vers la turbulence, etc.

« Constructal » est un mot inventé par Adrian Bejan, du verbe latin construere (construire), afin de désigner, du point de vue de sa théorie, les formes naturellement optimisées au travers du temps telles que les réseaux hydrologiques et les arbres mais aussi les formes ingéniérées provenant d'un processus évolutionniste de maximisation de l’accès du flux dans le temps.

Principes

La méthode constructale suit trois étapes : déterminer la forme élémentaire, en assembler plusieurs et faire émerger la forme globale^[1]. Par exemple, dans les systèmes flux d'un point vers une surface ou d'un point vers un volume, la théorie constructale prévoit des architectures arborescentes, ces flux devant présenter au moins deux régimes résistifs distincts. La théorie s'applique de plus à toutes les échelles : depuis les systèmes microscopiques aux macroscopiques.

Un principe important de la théorie constructale est de considérer que tous les systèmes sont destinés à demeurer imparfaits du fait de l'existence inévitable de résistances internes (frottements, etc.). D'un point de vue constructal, le mieux que l'on puisse faire est de distribuer de manière optimale ces imperfections, et c'est précisément de cette distribution optimale des imperfections que la forme du système émerge spontanément.

En particulier l'une des façons de distribuer de manière optimale ces imperfections consiste à distribuer le régime le plus résistant du système à l'échelle la plus petite du système.

Le principe constructal a été énoncé comme suit par Adrian Bejan en 1996 : « Pour qu'un système fini puisse persister dans le temps, il doit évoluer de manière à offrir un accès facilité aux flux qui le traversent ». La Loi constructale est le principe qui génère la forme « parfaite », qui est en fait la forme la moins imparfaite possible.

Résultats

La théorie constructale est prédictive et a donc pu être vérifiée.

Loi allométrique entre la vitesse de vol et la masse corporelle

Le principe constructal d'architecture de flux arborescent a ainsi permit de prédire de manière totalement déterministe de nombreuses lois allométriques empiriques, par exemple:

• la loi de Kleiber de proportionnalité entre le taux métabolique q₀ et la masse corporelle M élevée à la puissance 3/4 :
• la proportionnalité entre les périodes respiratoire et de battement du cœur t et la masse corporelleM élevée à la puissance 1/4 :
• la proportionnalité entre la surface de contact de transfert A et la masse corporelle M :
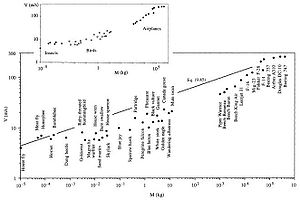
• la proportionnalité entre la vitesse optimale de vol V_opt (en ms ^{− 1}) des corps volants (insectes, oiseaux, aéronefs) et la masse M (en kg) élevée à la puissance 1/6 :

La Loi constructale de Bejan explique aussi pourquoi les bronches présentent une arborescence avec 23 niveaux de bifurcations. Le modèle constructal d'architecture des bronches a ainsi délivré de manière déterministe :

• les dimensions des sacs alvéolaires,
• la surface totale des voies aériennes,
• la surface alvéolaire totale,
• la résistance totale du transport d'oxygène dans l'arbre respiratoire.

Notes et références

Voir aussi

• Adrian Bejan
• Mécanique
• Fractale

Liens externes

• Portail internet de la Théorie Constructale : publications, événements, liens, etc.
• Description de la théorie par son auteur (principalement en anglais)

Références

• Shape and Structure, from Engineering to Nature , Cambridge University Press, Cambridge, UK, 2000. ISBN 0521793882
• Proceedings of the Symposium « Bejan’s Constructal Theory of Shape and Structure » Edited by Rui N. Rosa, A. Heitor Reis & A. F. Miguel, Centro de Geofísica de Évora, Évora Geophysics Center, Portugal, 2004, ISBN 972-9039-75-5
• A. Bejan, Constructal theory of organization in nature: dendritic flows, allometric laws and flight, Design and Nature, CA Brebbia, L Sucharov & P Pascola (Editors). ISBN 1-85312-901-1
• A. H. Reis, A. F. Miguel , M. Aydin, Constructal theory of flow architecture of the lungs, Journal of Medical Physics, May 2004, Volume 31, Issue 5, pp. 1135-1140.
• A. H. Reis, A. Bejan, Constructal theory of global circulation and climate, International Journal of Heat and Mass Transfer.
• A.Bejan, S. Lorente, La loi constructale, Traduction et avant-propos d'A. Kremer-Marietti, Paris, L'Harmattan, 2005.
• Teresa Mia Bejan, « Natural law and natural design », février 2005, http://dogma.free.fr/txt/TB-NaturalDesign.htm
• Angèle Kremer-Marietti, « The constructal principle », juillet 2006,http://dogma.free.fr/txt/AKM-ConstructalPrinciple.htm
• Abdelkader Bachta, "Science et technique: la géométrie et la physique de la loi constructale", 2007, http://dogma.free.fr/txt/AB-ScienceTechnique.htm
• Abdelkader Bachta, Jean Dhombres, Angèle Kremer-Marietti, Trois Etudes sur la loi constructale d'Adrian Bejan, Paris, L'Harmattan, 2008.
• Adrian Bejan, Sylvie Lorente, Design with Constructal Theory, Hoboken (New Jersey-USA), Wiley, September 2008, 552p. ISBN 978-0-471-99816-7