Résistance à la rupture

Résistance à la rupture

La résistance à la rupture d’un matériau caractérise la contrainte maximale qu’il peut subir avant de se rompre ou de subir une déformation permanente.

Cette phase passe après deux étapes successives :

  • la déformation élastique  : c’est la déformation non permanente que subit un matériau sous une certaine contrainte. Le matériau reprenant sa forme initiale dés que cesse cette contrainte ;
  • la déformation permanente  : le matériau a atteint la limite élastique et ne reprend pas sa forme initiale,

Sommaire

Types de sollicitations

Pour un même matériau, cette résistance à la rupture dépend du type de sollicitation ou de fatigue qu’il subit.

Traction ou extension

Pour qu’une pièce sollicitée à l’extension par une force F résiste en toute sécurité, il faut que la contrainte normale : \sigma = {F \over S}, soit inférieure ou au plus égale à la résistance pratique à l’extension Rp

Rp \geqslant{F \over S}

avec :

σ = la contrainte normale ;
Rp = la résistance pratique à l’extension ;
F = la force tangentielle appliquée (N) ;
S = la section mini du matériau (mm2).

Compression

Comme pour l’extension, une pièce courte comprimée doit avoir une contrainte pratique à la compression inférieure à la résistance pratique du matériau.

Rp \geqslant{F \over S}

Flambage

Sollicitation au flambage
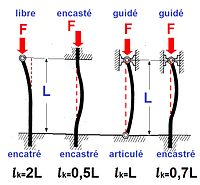
Article détaillé : Flambage.

La charge critique de flambage F est la charge pour laquelle la limite d’élasticité à la compression est atteinte dans la pièce. Son expression est donnée par la formule d'Euler :

F=\frac{\pi^2 E I}{l_k^2}

où

Flexion

Rp \geqslant{Mf \over {Io\over v}}

avec :

Rp = la résistance pratique ;
Mf = le moment de flexion (mm.N) ;
Io\over v = module de flexion de la section du matériau (mm2).

Torsion

Rpg \geqslant{Mt \over {Io\over v}}
Rpg = la résistance pratique au cisaillement ;
Mt = le moment de torsion (mm.N) ;
Io\over v = module de torsion de la section du matériau (mm2).

Flexion + torsion

Flexion et torsion simultanées

Lorsqu’un arbre de transmission subit à la fois une torsion et une flexion, son diamètre d pourra être calculé comme s’il était uniquement sollicité à la flexion par un couple de moment M qui tient compte des moments Mf et Mt :

M = 0,35 Mf + 0,65 \sqrt{Mf^2 + Mt^2}

d’où

Rp \geqslant{M \over {Io\over v}}.

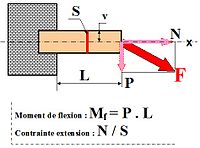
Flexion + extension

Flexion et extension simultanées
Rp \geqslant{Mf \over {Io\over v}} + {F\over S}

avec :

Rp = la résistance pratique ;
Mf = le moment de flexion (mm.N) ;
Io\over v = module d'inertie de la section du matériau (mm2) ;
Article détaillé : Module d'inertie.
F force résultante dans l’axe de la pièce et qui tend à l’allonger ;
S = la section mini du matériau (mm2).

Cisaillement

Rpg \geqslant{F \over S}

avec :

Rpg = la résistance pratique au glissement ;
F = la force tangentielle appliquée (N) au droit de la section ;
S = la section du matériau (mm2) au droit de la force.

Torsion + cisaillement

Torsion et cisaillement
Rpg \geqslant{Mt \over {Io\over v}} + {F\over S}

avec :

Rpg = la résistance pratique au cisaillement ;
Mt = le moment de torsion (mm.N) ;
Io\over v = module d'inertie (torsion) de la section du matériau (mm2) ;
Article détaillé : Module d'inertie.
F force de flexion (N) ;
S = la section mini du matériau (mm2).

Liens internes


Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Résistance à la rupture de Wikipédia en français (auteurs)

Игры ⚽ Поможем решить контрольную работу

Regardez d'autres dictionnaires:

  • résistance à la rupture — stiprumo riba statusas T sritis fizika atitikmenys: angl. strength limit vok. Bruchgrenze, f; Festigkeitsgrenze, f rus. предел прочности, m pranc. limite de rupture, f; résistance à la rupture, f; résistance limite, f …   Fizikos terminų žodynas

  • résistance à la rupture — trūkstamasis stiprumas statusas T sritis fizika atitikmenys: angl. breaking strength; rupture strength vok. Bruchfestigkeit, f; Zerreißfestigkeit, f rus. прочность на разрыв, f; прочность при разрыве, f pranc. résistance à la rupture, f …   Fizikos terminų žodynas

  • résistance à la rupture — stiprio riba statusas T sritis Standartizacija ir metrologija apibrėžtis Ribinis medžiagos stipris, išreikštas ardomosios jėgos ir ploto, kurį veikė ši jėga, dalmeniu. atitikmenys: angl. ultimate strength vok. Festigkeit, f; Festigkeitsgrenze, f… …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

  • résistance — [ rezistɑ̃s ] n. f. • resistence 1270; de résister I ♦ Phénomène physique consistant dans l opposition à une action ou à un mouvement. 1 ♦ Fait de résister, d opposer une force (à une autre), de ne pas subir les effets (d une action). Résistance… …   Encyclopédie Universelle

  • rupture — [ ryptyr ] n. f. • XIVe; lat. ruptura, de rumpere « rompre » → roture 1 ♦ Division, séparation brusque (d une chose solide) en deux ou plusieurs parties; son résultat. ⇒ brisement, fracture. Rupture d essieu. Mécan. Division d un solide en deux… …   Encyclopédie Universelle

  • Rupture du ligament croisé — Traduction à relire Kreuzbandriss → …   Wikipédia en Français

  • Résistance à la traction — Essai de traction courbe de traction typique d un matériau ductile Un essai de traction est une expérience de physique qui permet de mesurer le degré de résistance à la rupture d un matériau quelconque. Certains objets fabriqués par l homme… …   Wikipédia en Français

  • Résistance — Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : « Résistance », sur le Wiktionnaire (dictionnaire universel) Sommaire …   Wikipédia en Français

  • résistance limite — stiprumo riba statusas T sritis fizika atitikmenys: angl. strength limit vok. Bruchgrenze, f; Festigkeitsgrenze, f rus. предел прочности, m pranc. limite de rupture, f; résistance à la rupture, f; résistance limite, f …   Fizikos terminų žodynas

  • rupture strength — trūkstamasis stiprumas statusas T sritis fizika atitikmenys: angl. breaking strength; rupture strength vok. Bruchfestigkeit, f; Zerreißfestigkeit, f rus. прочность на разрыв, f; прочность при разрыве, f pranc. résistance à la rupture, f …   Fizikos terminų žodynas

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”