Nombre domatique
- Nombre domatique
-
En théorie des graphes, le nombre domatique d'un graphe est son nombre maximum d'ensembles dominants disjoints deux à deux. Le problème du nombre domatique est de déterminer, en fonction d'un graphe G et d'un entier naturel k, si le nombre domatique de G est supérieur ou égal à k. C'est un problème NP-complet.
Exemple
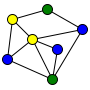
Le nombre domatique de ce graphe vaut au moins 3.
Dans le graphe ci-contre, les trois ensembles de sommets (associés à chaque couleur) sont disjoints deux à deux, et dominants (par exemple pour l'ensemble jaune : tout sommet est soit jaune, soit voisin d'un jaune). Le nombre domatique du graphe vaut donc au moins 3 (en fait, il est exactement égal à 3).
Définitions équivalentes
Le nombre domatique de G est le plus grand entier n pour lequel il existe une partition de l'ensemble des sommets en n ensembles dominants.
Le problème du nombre domatique pour G et k revient à déterminer s'il existe k ensembles dominants disjoints deux à deux.
Complexité
Le problème du nombre domatique a été prouvé NP-complet par réduction mutuelle avec le problème 3SAT.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Domatic number problem » (voir la liste des auteurs)
- (en) Michael Garey (en) et David S. Johnson (en), Computers and Intractability (en), W.H. Freeman, 1979. A1.1: GT2, p 190 (ISBN 0-7167-1045-5)
- (en) E. J. Cockayne et S. T. Hedetniemi, "Optimal domination in graphs", IEEE Trans. Circuits and Systems CAS-22, 855-857
Wikimedia Foundation.
2010.
Contenu soumis à la licence CC-BY-SA. Source : Article Nombre domatique de Wikipédia en français (auteurs)
Regardez d'autres dictionnaires:
Probleme du nombre domatique — Problème du nombre domatique Le problème du nombre domatique est un problème NP complet de la théorie des graphes. Définition Une instance du problème du nombre domatique consiste en un graphe G avec un ensemble S de sommets et un ensemble A d… … Wikipédia en Français
Problème du nombre domatique — Le problème du nombre domatique est un problème NP complet de la théorie des graphes. Définition Une instance du problème du nombre domatique consiste en un graphe G avec un ensemble S de sommets et un ensemble A d arcs, et un entier positif k… … Wikipédia en Français
Liste de problèmes NP-complets — Ceci est une liste des problèmes NP complets les plus connus en théorie de la complexité des algorithmes, exprimés sous la forme d un problème de décision. Puisqu on connaît plus de 3000 problèmes NP complets, cette liste n est pas exhaustive. La … Wikipédia en Français
Liste De Problèmes NP-Complets — Ceci est une liste des problèmes NP complets les plus connus en théorie de la complexité des algorithmes, exprimés sous la forme d un problèmes de la décision. Puisqu on connaît plus de 3000 problèmes NP complets, cette liste n est pas exhaustive … Wikipédia en Français
Liste de problemes NP-complets — Liste de problèmes NP complets Ceci est une liste des problèmes NP complets les plus connus en théorie de la complexité des algorithmes, exprimés sous la forme d un problèmes de la décision. Puisqu on connaît plus de 3000 problèmes NP complets,… … Wikipédia en Français
Liste de problèmes np-complets — Ceci est une liste des problèmes NP complets les plus connus en théorie de la complexité des algorithmes, exprimés sous la forme d un problèmes de la décision. Puisqu on connaît plus de 3000 problèmes NP complets, cette liste n est pas exhaustive … Wikipédia en Français
Langite — Langite[1] Catégorie VII : sulfates, sélénates tellurates, chromates, molybdates, tungstates[2] … Wikipédia en Français

