- Ensemble dominant
-
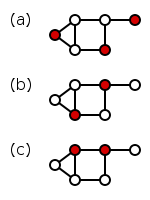
En théorie des graphes, un ensemble dominant d'un graphe G = ( S, A ) est un sous-ensemble D de l'ensemble S des sommets tel que tout sommet qui n'appartient pas à D possède au moins une arête commune avec un sommet de D. Le problème d'ensemble dominant est de déterminer, en fonction de G et d'un entier naturel k, si G possède un ensemble dominant d'au plus k sommets. Ce problème est NP-complet.
Un graphe avec trois exemples d'ensembles dominants (constitués des sommets rouges).Sommaire
Exemples et remarques
- Si l'on exclut le cas du graphe vide, un ensemble dominant est nécessairement non vide.
- L'ensemble S de tous les sommets est toujours dominant.
- Par conséquent, le problème ne se pose vraiment que pour k strictement positif et strictement inférieur au nombre de sommets du graphe.
NP-complétude
Le problème d'ensemble dominant a été prouvé NP-complet par réduction mutuelle avec le problème de couverture de sommets. En effet, les problèmes de couverture de sommets et d'ensemble dominant sont similaires, la différence étant que le premier concerne des arcs alors que le second concerne les sommets.
Couverture de sommets vers ensemble dominant
Les couvertures de sommets du graphe G correspondent aux ensembles dominants du graphe G' construit à partir de G
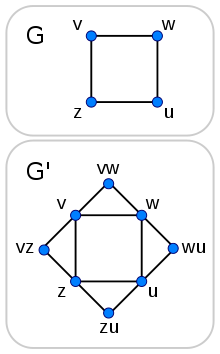
Soit <G, k> une instance du problème de couverture de sommets. On construit (cf figure ci-contre) un nouveau graphe G' , en ajoutant à G de nouveaux sommets, pour représenter les arcs du graphe initial G. Précisément, pour tout arc <v, w> de G, ajoutons un sommet vw et les arcs <v, vw> et <w,vw>.
Montrons qu'alors, G' a un ensemble dominant D de taille k si et seulement si G a une couverture de sommets C de taille k.
(
) D est un ensemble dominant de G' de taille k. Donc, tout arc de G' concerne un sommet de D. D est donc une couverture des sommets de G de taille k.(
) C est une couverture de sommets de G de taille k, donc les nouveaux et les anciens sommets sont dominés par k sommets.Ensemble dominant vers couverture de sommets
Approximation
La version « optimisation » du problème, qui consiste à trouver un ensemble dominant D tel que | D | soit minimum, est approximable. Pour être plus précis, il est approximable avec un facteur 1 + log | D | . Cependant, il n'est pas approximable à une distance clog | D | pour un c > 0.
Références
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Dominating set problem » (voir la liste des auteurs)
- (en) Michael Garey (en) et David S. Johnson (en), Computers and Intractability (en), W. H. Freeman, 1979 (ISBN 0-7167-1045-5) A1.1, GT2, p 190
- (en) S. Mitchell et S. Hedetniemi, Edge domination in trees, Proceedings of the 8th Southeastern Conference on Combinatorics, Graph Theory, and Computing (1977) Utilitas Mathematica Publishing, Winnipeg, 489-509
- (en) M. Yannakakis et F. Gavril, Edge dominating sets in graphs (1978) manuscrit non publié.
- (en) Minimum dominating set, une page du Compendium of NP optimization problems de P. Crescenzi et V. Kann
Wikimedia Foundation. 2010.
