Beau théorème de Gauss

Le Theorema Egregium (« théorème remarquable » en latin) est un important théorème énoncé par Carl Friedrich Gauss et portant sur la courbure des surfaces. Il dit que celle-ci peut être entièrement déterminée en mesurant les angles et les distances d'une surface, c'est-à-dire qu'elle ne dépend pas de la manière dont la surface peut être plongée dans l'espace tridimensionnel.

Énoncé

Considérons une surface de l'espace euclidien 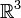. La distance intrinsèque entre deux points est définie comme l'infimum des longueurs des courbes tracées sur la surface et joignant ces deux points. (par exemple la distance intrinsèque de deux points opposés de la sphère unité est 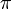, alors que leur distance euclidienne est 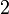. Une courbe minimisant la longueur entre deux points s'appelle une géodésique.

Deux surfaces sont isométriques s'il existe une bijection entre les deux surfaces préservant la distance. Elles sont localement isométriques s'il existe une telle bijection définie au voisinage d'un point.

La courbure de Gauss d'une surface s'obtient de plusieurs manières:

comme le produit du maximum et du minimum de la courbure d'une géodésique passant par ce point, ou, ce qui revient au même, de la courbure en ce point des intersections de la surface avec les plans passant par la normale

comme le rapport entre l'aire d'un voisinage infinitésimal du point et l'aire de son image sur la sphère par l'application normale.

Dans ces deux définitions, on voit que la courbure de Gauss dépend, a priori de la manière dont la surface est plongée dans l'espace: on peut obtenir des surfaces localement isométriques par des plongements distincts de la surface dans l'espace. L'exemple le plus simple est donné par l'exemple du plan et la surface d'un cylindre :

comme on peut enrouler une feuille de papier plane sur un cylindre, on obtient une isométrie locale du plan sur le cylindre. En effet la déformation (sans froissage) d'une feuille de papier ne modifie pas la distance entre deux points proches.

En langage moderne, le théorème peut s'énoncer ainsi:

La courbure de Gauss d'une surface est invariante par isométrie locale.

Ce théorème est remarquable car la définition de la courbure de Gauss utilise directement le plongement de la surface dans l'espace. Il est donc assez étonnant que le résultat final ne dépende pas du plongement.

La démonstration est subtile, et pas toujours transparente : si on représente la surface par une équation, ou mieux, une représentation paramétrique, ce qui est caché derrière est une commutation de dérivées d'ordre 3.

Applications simples

Il est impossible de plier une feuille de papier pour en faire une sphère. Plus formellement, le plan et la 2-sphère ne sont pas localement isométriques. Ceci provient du fait que le plan a une courbure de Gauss constante égale à 0 tandis qu'aucun point de la sphère n'a une courbure nulle. (On peut pourtant démontrer ce fait plus directement).

Des points correspondants sur une caténoïde et une hélicoïde (deux surfaces d'aspect très différent) ont la même courbure de Gauss. (Ces deux surfaces sont localement isométriques).

Voir aussi

• M. Audin, Géométrie, Belin 1998, ISBN 2-7011-2130-2
• M. Berger, A panoramic view of Riemannian Geometry, Springer

• Portail de la géométrie