Fonctions d'Argyris

Fonctions d'Argyris: Les fonctions d’Argyris (ou éléments d’Argyris) sont un outil en méthodes des éléments finis. Elles sont utilisées pour décrire un polynôme dans un triangle d’un maillage en employant seulement des données connues sur le bord du triangle (comme les valeurs au sommet, les valeurs des dérivées premières et secondes au sommet, ainsi que les valeurs « liées aux arêtes »). l'avantage est que l'on peut se ramener à un espace de dimension finie que l'on peut utilisé pour le calcul numérique.

Utilisées en modélisation numérique, ces fonctions furent introduites dans les années 1950 ; mais d'autres styles de fonctions sont également employées en pratique en fonction des problèmes à résoudre.

Sommaire

1 Introduction

1.1 Contexte

1.2 Cadre d’étude

1.3 Approche formelle

2 Exemple

3 Matrice de passage

3.1 Notations

3.1.1 Construction de la matrice C

4 Logiciels gérant les éléments d’Argyris

5 Bibliographie

6 Notes et références

7 Voir aussi

Introduction

Contexte

John Hadji Argyris (en) (1913-2004)^[1]^,^[2] est l’un des précurseurs dans le domaine des méthodes des éléments finis, utilisée lors de résolution numérique d’équations différentielles issues de la physique, mécanique… comme la théorie des plaques. Ses concepts sont apparus en premier lors de la Seconde Guerre Mondiale, ce qui rendait ses premiers résultats top secret.

Le principe des fonctions d'Argyris consiste à exprimer un polynôme avec pour seules informations des données relatives au maillage du domaine. Bien évidemment, d'autres fonctions sont utilisées en Méthodes des Eléments Finis (Lagrange, Raviart-Thomas, Nédélec, GaussLobatto, Hermite, Morley, Bell…) ayant chacune leurs avantages ainsi que leurs inconvénients (tout dépend du problème que l'on veut résoudre).

Les éléments d'Argyris sont exclusivement dénommés ainsi pour la dimension 2 ( ${}^{\R^2}$ ). En dimension 1, voire 3, on parle plutôt d'éléments de type Argyris.

Cadre d’étude

On se place dans ${}^{\R^2}$ . Les variables sont appelées $x$ et $y$ . Soit $T$ un triangle quelconque, non aplati.

Les fonctions d'Argyris liées à $T$ sont des fonctions de base de l'espace vectoriel $\mathbb{P}_5(T)$ qui représente l'ensemble des polynômes à deux variables $x$ et $y$ ( $(x,y) \in T$ ) de degré au plus 5.

Approche formelle

Un élément $M \in \mathbb{P}_5(T)$ s'écrit de manière unique sous la forme

$M = a 0 + a 1 x + b 1 y + a 2 x 2 + b 2 x y + c 2 y 2 + a 3 x 3 + b 3 x 2 y + c 3 x y 2 + d 3 y 3 + a 4 x 4 + b 4 x 3 y + c 4 x 2 y 2 + d 4 x y 3 + e 4 y 4 + a 5 x 5 + b 5 x 4 y + c 5 x 3 y 2 + d 5 x 2 y 3 + e 5 x y 4 + f 5 y 5$ .

Ainsi, la seule donnée des coefficients $a_0\,,\,a_1\,,\,a_2\,,\,a_3\,,\,a_4\,,\,a_5\,,\,b_1\,,\,b_2\,,\,b_3\,,\,b_4\,,\,b_5\,,\,c_2\,,\,c_3\,,\,c_4\,,\,c_5\,,\,d_3\,,\,d_4\,,\,d_5\,,\,e_4\,,\,e_5\,,\,f_5$ suffit à écrire tout élément de $\mathbb{P}_5(T)$ . C'est pourquoi l'espace $\mathbb{P}_5(T)$ est un espace de dimension 21 (nombre de coefficients à déterminer).

Il nous faut alors 21 relations (conditions) indépendantes afin de pouvoir déterminer ces 21 coefficients : on appelle cela les degrés de liberté.

Une base possible est ${1, x, y, x 2, x y, y 2, x 3, x 2, y 2, y 3, x 4, x 3 y, x 2 y 2, x y 3, y 4, x 5, x 4 y, x 3 y 2, x 2 y 3, x y 4, y 5}$ : on l'appelle la base canonique.

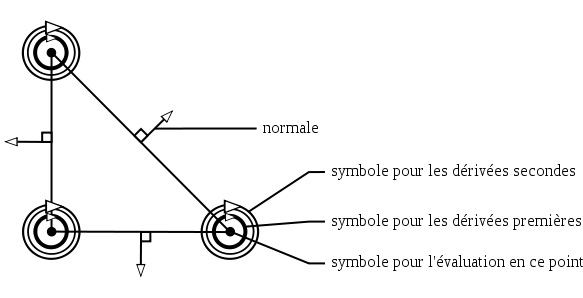
Dans la pratique, il est extrêmement difficile (et surtout pas pratique) de pouvoir trouver les 21 coefficients avec cette base. C'est pourquoi nous formulons une base différente formée des fonctions d'Argyris. Elles sont liées à des conditions données :

sur la valeur de la fonction M en chaque sommet (3 relations);

sur la valeur des dérivées premières de la fonction M en chaque sommet (6 relations);

sur la valeur des dérivées secondes de la fonction M en chaque sommet (9 relations);

sur la valeur "liée à la normale" pour chaque arête (3 relations).

Remarque 1 : Ces conditions ne sont pas uniques : on peut toujours trouver d'autres conditions, mais celles-ci sont les plus simples à mettre en application.

Remarque 2 : Le dernier point concerne la valeur "liée à la normale". C'est une définition un peu particulière qui peut être différente selon les travaux. Vous trouverez ici une définition possible et qui est la plus couramment utilisée.

Avec ces données, il est possible de calculer toutes les fonctions d'Argyris pour n'importe quel triangle : il suffit pour cela de résoudre un système linéaire AU=B où :

A est une matrice 21*21;

U est un vecteur de taille 21 composé des 21 coefficients;

B est un vecteur de taille 21 dont toutes les composantes sont nulles sauf une qui correspond à la condition adéquate.

Vous pourrez trouver un exemple de fonctions d'Argyris dans la partie Exemple avec les conditions indiquées entre parenthèses.

Remarque 3 : Résoudre ce système est équivalent à inverser la matrice A.

En pratique, il est impensable de calculer toutes les fonctions de bases pour chaque triangle car le nombre de triangles peut être énorme (de l'ordre de plusieurs millions par exemple). C'est pourquoi, on calcule les fonctions sur un triangle particulier dit triangle de référence ayant pour sommets les points (0;0), (1;0),(0;1) et on en « déduit » les fonctions d'Argyris dans un triangle particulier.

Exemple

Voici la liste des fonctions de base d'Argyris dans le triangle de référence avec la condition correspondante (cela signifie que le degré de liberté associé à la condition vaut 1 et que les autres valent 0).

$\begin{array}{ll} \varphi_{1}(x,y) = 1 - 10x^3 - 10y^3 + 15x^4 - 30x^2y^2 + 15y^4 - 6x^5 + 30x^3y^2 + 30x^2y^3 - 6y^5, & (\varphi_1(0,0) = 1), \\ \varphi_{2}(x,y) = 10x^3 - 15x^4 + 15x^2y^2 + 6x^5 - 15x^3y^2 - 15x^2y^3, & (\varphi_2(1,0) = 1),\\ \varphi_{3}(x,y) = 10y^3 + 15x^2y^2 - 15y^4 - 15x^3y^2 - 15x^2y^3 + 6y^5, & (\varphi_{3}(0,1) = 1),\\ \varphi_{4}(x,y) = x - 6x^3 - 11xy^2 + 8x^4 + 10x^2y^2 + 18xy^3 - 3x^5 + x^3y^2 - 10x^2y^3 - 8xy^4, & (\partial_x\varphi_4(0,0) = 1),\\ \varphi_{5}(x,y) = y - 11x^2y - 6y^3 + 18x^3y + 10x^2y^2 + 8y^4 - 8x^4y - 10x^3y^2 + x^2y^3 - 3y^5, & (\partial_y\varphi_5(0,0) = 1),\\ \varphi_{6}(x,y) = -4x^3 + 7x^4 - 3.5x^2y^2 - 3x^5 + 3.5x^3y^2 + 3.5x^2y^3, & (\partial_x\varphi_6(1,0) = 1),\\ \varphi_{7}(x,y) = -5x^2y + 14x^3y + 18.5x^2y^2 - 8x^4y - 18.5x^3y^2 - 13.5x^2y^3, & (\partial_y\varphi_7(1,0) = 1),\\ \varphi_{8}(x,y) = -5xy^2 + 18.5x^2y^2 + 14xy^3 - 13.5x^3y^2 - 18.5x^2y^3 - 8xy^4, & (\partial_x\varphi_{8}(0,1) = 1),\\ \varphi_{9}(x,y) = -4y^3 - 3.5x^2y^2 + 7y^4 + 3.5x^3y^2 + 3.5x^2y^3 - 3y^5, & (\partial_y\varphi_{9}(0,0) = 1),\\ \varphi_{10}(x,y) = 0.5x^2 - 1.5x^3 + 1.5x^4 - 1.5x^2y^2 - 0.5x^5 + 1.5x^3y^2 + x^2y^3, & (\partial^2_{xx}\varphi_{10}(0,0) = 1),\\ \varphi_{11}(x,y) = xy - 4x^2y - 4xy^2 + 5x^3y + 10x^2y^2 + 5xy^3 - 2x^4y - 6x^3y^2 - 6x^2y^3 - 2xy^4, & (\partial^2_{xy}\varphi_{11}(0,0) = 1),\\ \varphi_{12}(x,y) = 0.5y^2 - 1.5y^3 - 1.5x^2y^2 + 1.5y^4 + x^3y^2 + 1.5x^2y^3 - 0.5y^5, & (\partial^2_{yy}\varphi_{12}(0,0) = 1),\\ \varphi_{13}(x,y) = 0.5x^3 - x^4 + 0.25x^2y^2 + 0.5x^5 - 0.25x^3y^2 - 0.25x^2y^3, & (\partial^2_{xx}\varphi_{13}(1,0) = 1),\\ \varphi_{14}(x,y) = x^2y - 3x^3y - 3.5x^2y^2 + 2x^4y + 3.5x^3y^2 + 2.5x^2y^3, & (\partial^2_{xy}\varphi_{14}(1,0) = 1),\\ \varphi_{15}(x,y) = 1.25x^2y^2 - 0.75x^3y^2 - 1.25x^2y^3, & (\partial^2_{yy}\varphi_{15}(1,0) = 1),\\ \varphi_{16}(x,y) = 1.25x^2y^2 - 1.25x^3y^2 - 0.75x^2y^3, & (\partial^2_{xx}\varphi_{16}(0,1) = 1),\\ \varphi_{17}(x,y) = xy^2 - 3.5x^2y^2 - 3xy^3 + 2.5x^3y^2 + 3.5x^2y^3 + 2xy^4, & (\partial^2_{xy}\varphi_{17}(0,1) = 1),\\ \varphi_{18}(x,y) = 0.5y^3 + 0.25x^2y^2 - y^4 - 0.25x^3y^2 - 0.25x^2y^3 + 0.5y^5, & (\partial^2_{yy}\varphi_{18}(0,1) = 1),\\ \varphi_{19}(x,y) = \sqrt{2}(-8x^2y^2 + 8x^3y^2 + 8x^2y^3),& \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!(\sqrt{0.5}(\partial_{x}\varphi_{19}(0.5,0.5) + \partial_{y}\varphi_{19}(0.5,0.5)) = 1),\\ \varphi_{20}(x,y) = -16xy^2 + 32x^2y^2 + 32xy^3 - 16x^3y^2 - 32x^2y^3 - 16xy^4, &(-\partial_{x}\varphi_{20}(0,0.5) = 1),\\ \varphi_{21}(x,y) = -16x^2y + 32x^3y + 32x^2y^2 - 16x^4y - 32x^3y^2 - 16x^2y^3, &(-\partial_{y}\varphi_{21}(0.5,0) = 1),\\ \end{array}$

Remarque 4 : L’ordre n’a a priori aucune importance. Pour la programmation (ou l’utilisation de manière générale), il faut néanmoins se fixer un ordre et le conserver tout le temps.

Explications :

La condition concernant la normale est $(\partial_{x}\varphi(m_e) + \partial_{y}\varphi(me)) \cdot n_e$ , où $m e$ représente le milieu de l'arête $e$ et $n e$ désigne la normale à l'arête $e$ sortante du triangle.

Expliquons maintenant comment se forme la matrice $A$ .

Tout d'abord, le vecteur colonne $U$ est composé des coefficients à déterminer, c'est-à-dire $U=(a_0\,;\,a_1\,;\,b_1\,;\,a_2\,;\,b_2\,;\,c_2\,;\,a_3\,;\,b_3\,;\,c_3\,;\,d_3\,;\,a_4\,;\,b_4\,;\,c_4\,;\,d_4\,;\,e_4\,;\,a_5\,;\,b_5\,;\,c_5\,;\,d_5\,;\,e_5\,;\,f_5)$ .

Voyons comment se compose, par exemple, les lignes 1 et 6 de la matrice liées aux conditions $φ(0,0) = 1$ et $\partial_x\varphi(1,0) = 1$ (les autres étant similaires).

$\left. \begin{array}{l} \varphi_1(x,y)=a_0+a_1x+b_1y+a_2 x^2+b_2 xy+c_2 y^2+a_3 x^3+b_3 x^2 y+c_3 x y^2+d_3 y^3+a_4x^4+b_4 x^3 y\\[4pt] \,\,\,\,\,\,\,\,+c_4 x^2 y^2+d_4 x y^3+e_4 y^4+a_5 x^5+b_5 x^4 y+c_5 x^3 y^2+d_5 x^2 y^3 + e_5 x y^4+f_5 y^5\\[6pt] \Rightarrow \varphi_1(0,0)=a_0. \end{array} \right.$

Donc la première ligne de la matrice M est $(1,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0)$ .

$\left. \begin{array}{l} \varphi_6(x,y)=a_0+a_1x+b_1y+a_2 x^2+b_2 xy+c_2 y^2+a_3 x^3+b_3 x^2 y+c_3 x y^2+d_3 y^3+a_4x^4+b_4 x^3 y\\[4pt] \,\,\,\,\,\,\,\,+c_4 x^2 y^2+d_4 x y^3+e_4 y^4+a_5 x^5+b_5 x^4 y+c_5 x^3 y^2+d_5 x^2 y^3 + e_5 x y^4+f_5 y^5\\[6pt] \Rightarrow \partial_x \varphi_6(x,y)=a_1+2a_2 x+b_2 y+3a_3x^2+2b_3 xy+c_3y^2+4a_4x^3+3b_4x^2y+2c_4xy^2+d_4y^3\\[4pt] \,\,\,\,\,\,\,\,+5a_5x^4+4b_5x^3y+3c_5x^2y^2+2d_5xy^3+e_5y^4\\[6pt] \Rightarrow\partial_x \varphi_6(1,0)=a_1+2a_2+3a_3+4a_4+5a_5. \end{array}\right.$ .

Donc la sixième ligne de la matrice M est $(0,1,0,2,0,0,3,0,0,0,4,0,0,0,0,5,0,0,0,0,0)$ .

Matrice de passage

Remarque 5 : Cette construction n'est valable que pour le cas traité en exemple.

Pour trouver les fonctions de base d'Argyris dans un triangle donné, il faut multiplier le vecteur constitué des différentes fonctions dans le triangle de référence par une certaine matrice $C$ que l'on explicitera ici.

Soient trois points non-alignés $X i = (x i, y i)(i = 1,2,3)$ qui formeront notre triangle $T$ . Nous considérons la transformation affine $F T$ qui envoie un point du triangle de référence $\widehat{T}$ sur un point de $T$ (on note $\widehat{X}$ le point de coordonnées $(\widehat{x},\widehat{y})$ dans $\widehat{T}$ ) :

$F_T : \widehat{T} \rightarrow T$

$X=F_T(\widehat{X}) = B_T\widehat{X} + X_1 := \left( \begin{array}{ll} x_2-x_1 & x_3-x_1 \\ y_2-y_1 & y_3-y_1 \end{array} \right) \left( \begin{array}{l} \widehat{x}\\ \widehat{y} \end{array} \right) +\left( \begin{array}{l} x_1\\ y_1 \end{array} \right)$ .

Afin de simplifier l'écriture, nous notons : $B:=B_T:=\left( \begin{array}{ll} b_{11} & b_{12} \\ b_{21} & b_{22} \end{array} \right)$ .

Notations

Dans le reste de cette présentation, on utilisera des notations simplificatrices :

Pour tout $\alpha \in \mathbb{N}^*$ , on note $I α$ la matrice identité $\alpha \times \alpha$ (elle ne comporte que des $1$ sur la diagonale, les autres composantes valant $0$ );

Pour tout couple $(\alpha,\beta) \in \mathbb{N}^* \times \mathbb{N}^*$ , on note $0_{\alpha \times \beta}$ la matrice nulle $\alpha \times \beta$ (toutes ses composantes valent $0$ ).

On note $e 1$ (resp. $e 2$ ; $e 3$ ) l'arête ayant pour sommets les points $X 2$ et $X 3$ (resp. $X 3$ et $X 1$ ; $X 1$ et $X 2$ ). On note $| e i |$ la longueur de l'arête $e i$ , $i \in \{1,2,3\}$ . On a alors :

$|e_1|=\sqrt{(x_3-x_2)^2+(y_3-y_2)^2}$ ;

$|e_2|=\sqrt{(x_1-x_3)^2+(y_1-y_3)^2}$ ;

$|e_3|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$ ;

Soit la matrice $3 \times 3$
$\Theta:= \left( \begin{array}{ccc} b_{11}^2&2b_{11}b_{21}&b_{21}^2\\ b_{11}b_{12}&b_{11}b_{22}+b_{12}b_{21}&b_{21}b_{22}\\ b_{12}^2&2b_{12}b_{22}&b_{22}^2 \end{array} \right)$ .

Soit la matrice $3 \times 2$
$A:= \left( \begin{array}{ll} a_{11}&a_{12}\\ a_{21}&a_{22}\\ a_{31}&a_{32} \end{array} \right):= \left( \begin{array}{lll} |e_1|^{-2}&0&0\\ 0&|e_2|^{-2}&0\\ 0&0&|e_3|^{-2} \end{array} \right) \left( \begin{array}{ll} 1/\sqrt{2}&1/\sqrt{2}\\ -1&0\\ 0&-1 \end{array} \right) B^T$ ,
où $B^T:= \left( \begin{array}{ll} b_{11} & b_{21} \\ b_{12} & b_{22} \end{array} \right)$ .

Pour tout $i \in \{1;2;3\}$ , on définit :
$f_i=a_{i1}\,v_i^y-a_{i2}\,v_i^x$ et $g_i=a_{i1}\,v_i^x+a_{i2}\,v_i^y$ .

Enfin, on note :

$v_1=X_3-X_2=\left(\begin{array}{l}x_3-x_2\\y_3-y_2\end{array}\right):=\left(\begin{array}{c}v_1^x\\v_1^y \end{array}\right);$

$v_2=X_1-X_3=\left(\begin{array}{l}x_1-x_3\\y_1-y_3\end{array}\right):=\left(\begin{array}{c}v_2^x\\v_2^y \end{array}\right);$

$v_3=X_2-X_1=\left(\begin{array}{l}x_2-x_1\\y_2-y_1\end{array}\right):=\left(\begin{array}{c}v_3^x\\v_3^y \end{array}\right);$

et

$w_1=\left(\begin{array}{c}v_1^x\, v_1^x\\2\,v_1^x \,v_1^y\\v_1^y \,v_1^y\end{array}\right):=\left(\begin{array}{c}(x_3-x_2)^2\\2(x_3-x_2)(y_3-y_2)\\(y_3-y_2)^2\end{array}\right)$ ;

$w_2=\left(\begin{array}{c}v_2^x \,v_2^x\\2\,v_2^x\, v_2^y\\v_2^y \,v_2^y\end{array}\right):=\left(\begin{array}{c}(x_1-x_3)^2\\2(x_1-x_3)(y_1-y_3)\\(y_1-y_3)^2\end{array}\right)$ ;

$w_3=\left(\begin{array}{c}v_3^x \,v_3^x\\2\,v_3^x\, v_3^y\\v_3^y\, v_3^y\end{array}\right):=\left(\begin{array}{c}(x_2-x_1)^2\\2(x_2-x_1)(y_2-y_1)\\(y_2-y_1)^2\end{array}\right)$ .

Remarque 6 : Si $V$ est une vecteur ligne de taille $n$ , on utilisera la notation $V T$ pour l'écrire en tant que vecteur ligne de taille $n$ : cela s'appelle la matrice transposée du vecteur V (où encore le vecteur transposé de V). Exemple : $v_1^T=(v_1^x;v_1^y)$

Construction de la matrice $C$

La matrice $C$ se construit comme le produit de deux matrices $C = D * E$ , où

$D$ est une matrice $21 \times 24$ définie par :
$D:= \left( \begin{array}{l|l|l|l|l|l|l|l} I_3&0_{3 \times 2}&0_{3 \times 2}&0_{3 \times 2}&0_{3 \times 3}&0_{3 \times 3}&0_{3 \times 3}&0_{3 \times 6}\\ \hline 0_{2 \times 3}&B^T&0_{2 \times 2}&0_{2 \times 2}&0_{2 \times 3}&0_{2 \times 3}&0_{2 \times 3}&0_{2 \times 6}\\ \hline 0_{2 \times 3}&0_{2 \times 2}&B^T&0_{2 \times 2}&0_{2 \times 3}&0_{2 \times 3}&0_{2 \times 3}&0_{2 \times 6}\\ \hline 0_{2 \times 3}&0_{2 \times 2}&0_{2 \times 2}&B^T&0_{2 \times 3}&0_{2 \times 3}&0_{2 \times 3}&0_{2 \times 6}\\ \hline 0_{3 \times 3}&0_{3 \times 2}&0_{3 \times 2}&0_{3 \times 2}&\Theta&0_{3 \times 3}&0_{3 \times 3}&0_{3 \times 6}\\ \hline 0_{3 \times 3}&0_{3 \times 2}&0_{3 \times 2}&0_{3 \times 2}&0_{3 \times 3}&\Theta&0_{3 \times 3}&0_{3 \times 6}\\ \hline 0_{3 \times 3}&0_{3 \times 2}&0_{3 \times 2}&0_{3 \times 2}&0_{3 \times 3}&0_{3 \times 3}&\Theta&0_{3 \times 6}\\ \hline 0_{3 \times 3}&0_{3 \times 2}&0_{3 \times 2}&0_{3 \times 2}&0_{3 \times 3}&0_{3 \times 3}&0_{3 \times 3}&Q \end{array} \right)$ , où $Q:=\left(\begin{array}{ccc|ccc} f_1&0&0&g_1&0&0\\ 0&f_2&0&0&g_2&0\\ 0&0&f_3&0&0&g_3 \end{array} \right)$ .

$E$ est une matrice $24 \times 21$ définie par :

$E:=\left(\begin{array}{c|c} I_{18}&0_{18 \times 3}\\ \hline 0_{3 \times 18}&L\\ \hline T&0_{3 \times 0} \end{array} \right)$ ,
où

$L:=\left(\begin{array}{ccc} |e_1|&0&0\\ 0&|e_2|&0\\ 0&0&|e_3| \end{array} \right)$ ;

$T:=\left(\begin{array}{c|c|c} T_1&T_2&T_3 \end{array} \right)$ , où :

$T 1$ est une matrice $3 \times 3$ définie par $T_1:=\frac{15}{8}\left(\begin{array}{lll} 0&-1&1\\ 1&0&-1\\ -1&1&0 \end{array} \right)$ ;

$T 2$ est une matrice $3 \times 6$ définie par $T_2:=\frac{-7}{16}\left(\begin{array}{ccc} 0_{1 \times 2}&v_1^T&v_1^T\\ v_2^T&0_{1 \times 2}&v_2^T\\ v_3^T&v_3^T&0_{1 \times 2} \end{array} \right)$ ;*## $T 3$ est une matrice $3 \times 9$ définie par $T_3:=\frac{1}{32}\left(\begin{array}{ccc} 0_{1 \times 3}&-w_1^T&w_1^T\\ w_2^T&0_{1 \times 3}&-w_2^T\\ -w_3^T&w_3^T&0_{1 \times 3} \end{array} \right)$ .

Logiciels gérant les éléments d’Argyris

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue !

getfem++

matlab

Bibliographie

V. Girault, P.-A. Raviart. Finite Element Methods for Navier-Stokes Equations. Theory and algorithms. Springer Series in Computational Mathematics, 5. Springer-Verlag, Berlin, 1986.

S. Nicaise, K.Witowski and B. I. Wohlmuth. An a posteriori error estimator for the Lamé equation based on equilibrated fluxes. IMA Journal of Numerical Analysis, 28, no.2, pp 331-353, 2008.

Librairie de getfem++

V. Domínguez, F.J. Sayas. Algorithm 884: A simple MATLAB implementation of the Argyris element. ACM Trans. Math. Software 35, Article 16, 2008.

M. Okabe. Full-explicit interpolation formulas for the Argyris triangle. Comput. Methods Appl. Mech. Engrg. 106, no. 3, pp 381--394, 1993.

Notes et références

↑ (en) In memoriam to Professor John H. Argyris, par Thomas J.R. Hughes (en), J. Tinsley Oden (en) et Manolis Papadrakakis

↑ (en) John H. Argyris

Voir aussi

Polynômes de Lagrange

Polynômes d'Hermite

Méthode des éléments finis étendus

Portail des mathématiques

Catégories :
Fonction arithmétique
Mécanique des milieux continus
Équations différentielles numériques

Contenu soumis à la licence CC-BY-SA. Source : Article Fonctions d'Argyris de Wikipédia en français (auteurs)

Игры ⚽ Нужен реферат?

Regardez d'autres dictionnaires:

Projet:Mathématiques/Liste des articles de mathématiques — Cette page n est plus mise à jour depuis l arrêt de DumZiBoT. Pour demander sa remise en service, faire une requête sur WP:RBOT Cette page recense les articles relatifs aux mathématiques, qui sont liés aux portails de mathématiques, géométrie ou… … Wikipédia en Français
ORGANISATIONS (THÉORIE DES) — La théorie des organisations est née au début du siècle des efforts déployés par certains chefs d’entreprise, comme Taylor ou Fayol, pour dégager des principes d’administration et de direction du travail. Elle s’est développée tout… … Encyclopédie Universelle
SOCIOLOGIE - L’intervention — L’action consciente de praticiens des sciences sociales en vue de transformer les organisations et les systèmes sociaux est essentielle pour le développement de ces sciences dans la mesure où elle seule permet de tester la pertinence d’une… … Encyclopédie Universelle
ENTREPRISE - Réforme — L’entreprise fait l’objet d’une mise en question qui prend parfois l’allure d’un réquisitoire. Des critiques sont formulées sur les plans économique, humain, politique; des propositions de réformes sont faites avec plus ou moins de précision; la… … Encyclopédie Universelle
DÉRIVÉES PARTIELLES (ÉQUATIONS AUX) - Analyse numérique — Plus peut être que tout autre domaine des mathématiques, les équations aux dérivés partielles étaient prédisposées à bénéficier de l’utilisation des ordinateurs, pour de nombreuses raisons. La plus importante est leur intervention dans de… … Encyclopédie Universelle
29 mai — Éphémérides Mai 1er 2 3 4 5 6 7 8 9 10 11 12 … Wikipédia en Français

Dictionnaires et Encyclopédies sur 'Academic'

Fonctions d'Argyris

Sommaire

Introduction

Contexte

Cadre d’étude

Approche formelle

Exemple

Matrice de passage

Notations

Construction de la matrice $C$

Logiciels gérant les éléments d’Argyris

Bibliographie

Notes et références

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Dictionnaires et Encyclopédies sur 'Academic'

Wikipédia en Français

Fonctions d'Argyris

Sommaire

Introduction

Contexte

Cadre d’étude

Approche formelle

Exemple

Matrice de passage

Notations

Construction de la matrice C

Logiciels gérant les éléments d’Argyris

Bibliographie

Notes et références

Voir aussi

Regardez d'autres dictionnaires:

Share the article and excerpts

Direct link

Construction de la matrice $C$