Problème de l'ensemble dominant

Problème de l'ensemble dominant

Problème de l'ensemble dominant

Le problème d'ensemble dominant est un problème NP-complet de la théorie des graphes.

Sommaire

Définition

Une instance du problème d'ensemble dominant est défini par

  • un graphe G comprenant un ensemble S de sommets et un ensemble A d'arcs ;
  • un entier k strictement positif et inférieur ou égal au nombre de sommets dans G.

Il s'agit alors de déterminer s'il existe un ensemble dominant pour G, de taille inférieure ou égale à k. En d'autres termes, nous voulons savoir s'il existe un sous-ensemble D de S ayant une taille inférieure ou égale à k et tel que tous les sommets qui ne sont pas dans D soient reliés à au moins un sommet de D par un arc de A.

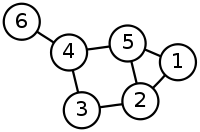
Exemple

6n-graf.svg

Pour le graphe sur la droite, {4,5} est un exemple d'ensemble dominant de taille 2.

NP-complétude

Le problème d'ensemble dominant a été prouvé NP-complet en utilisant une réduction depuis le problème de couverture de sommets.

Preuve

Les problèmes de couverture de sommets et d'ensemble dominant sont similaires ; la différence étant que le premier concerne des arcs alors que le second concerne les sommets. Par conséquent, trouvons un moyen pour construire un graphe utilisant des sommets pour représenter les arcs du graphe initial. Montrons comment construire le graphe permettant de faire la réduction du problème de couverture de sommets vers le problème d'ensemble dominant :

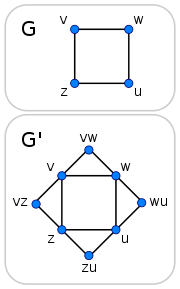
ReductionVCtoDS.svg

Soit <G, k> une instance du problème de couverture de sommets. Construisons un nouveau graphe G' en ajoutant de nouveaux sommets à G. Précisément, pour tout arc <v, w> de G, ajoutons un sommet vw et les arcs <v, vw> et <w,vw>.

Maintenant, la preuve : G' a un ensemble dominant D de taille k si et seulement si G a une couverture de sommets C de taille k.

(\Rightarrow) D est un ensemble dominant de G' de taille k. Donc, tout arc de G' concerne un sommet de D. D est donc une couverture des sommets de G de taille k.

(\Leftarrow) C est une couverture de sommets de G de taille k, donc les nouveaux et les anciens sommets sont dominés par k sommets.

Exemple

Le graphe sur la droite montre la construction du graphe G' pour faire la réduction.

Approximation

La version « optimisation » du problème, qui consiste à trouver le plus petit | D | tel que | D | soit un ensemble dominant, est approximable. Pour être plus précis, il est approximable avec un facteur 1 + log | D | , mais, attention, il n'est pas approximable à une distance clog | D | pour un c > 0.

Références

  • Michael R. Garey et David S. Johnson, Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, 1979. A1.1: GT2, p 190. (ISBN 0-7167-1045-5)
  • Mitchell S., and S. Hedetniemi [1977], "Edge domination in trees", Proceedings of the 8th Southeastern Conference on Combinatorics, Graph Theory, and Computing, Utilitas Mathematica Publishing, Winnipeg, 489-509.
  • Yannakakis, M. and F. Gavril [1978], "Edge dominating sets in graphs", manuscrit non publié.
  • (en) Un condensé de problèmes d'optimisation dans NP
Ce document provient de « Probl%C3%A8me de l%27ensemble dominant ».

Wikimedia Foundation. 2010.

Contenu soumis à la licence CC-BY-SA. Source : Article Problème de l'ensemble dominant de Wikipédia en français (auteurs)

Игры ⚽ Нужна курсовая?

Regardez d'autres dictionnaires:

  • Probleme de l'ensemble dominant — Problème de l ensemble dominant Le problème d ensemble dominant est un problème NP complet de la théorie des graphes. Sommaire 1 Définition 2 Exemple 3 NP complétude 3.1 Preuve …   Wikipédia en Français

  • Ensemble dominant — En théorie des graphes, un ensemble dominant d un graphe G = ( S, A ) est un sous ensemble D de l ensemble S des sommets tel que tout sommet qui n appartient pas à D possède au moins une arête commune avec un sommet de D. Le problème d ensemble… …   Wikipédia en Français

  • Probleme du nombre domatique — Problème du nombre domatique Le problème du nombre domatique est un problème NP complet de la théorie des graphes. Définition Une instance du problème du nombre domatique consiste en un graphe G avec un ensemble S de sommets et un ensemble A d… …   Wikipédia en Français

  • Problème du nombre domatique — Le problème du nombre domatique est un problème NP complet de la théorie des graphes. Définition Une instance du problème du nombre domatique consiste en un graphe G avec un ensemble S de sommets et un ensemble A d arcs, et un entier positif k… …   Wikipédia en Français

  • Problème NP-complet — En théorie de la complexité, un problème NP complet est un problème de décision vérifiant les propriétés suivantes : Il est possible de vérifier une solution efficacement (en temps polynomial) ; la classe des problèmes vérifiant cette… …   Wikipédia en Français

  • Problème christologique — Christologie La christologie est la discipline de la théologie dogmatique qui étudie la personne et les paroles de Jésus Christ, réfléchit sur la confession de foi chrétienne relative à Jésus Christ, à partir notamment de la signification et de l …   Wikipédia en Français

  • Graphe (mathématiques) — Théorie des graphes  Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une branche commune à l informatique et aux mathématiques étudiant les graphes et les objets qui lui… …   Wikipédia en Français

  • Graphe (théorie des graphes) — Théorie des graphes  Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une branche commune à l informatique et aux mathématiques étudiant les graphes et les objets qui lui… …   Wikipédia en Français

  • Theorie des graphes — Théorie des graphes  Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une branche commune à l informatique et aux mathématiques étudiant les graphes et les objets qui lui… …   Wikipédia en Français

  • Théorie des graphes — Pour la notion mathématique utilisée en Théorie des ensembles, voir Graphe d une fonction. La théorie des graphes est une théorie informatique et mathématique. Les algorithmes élaborés pour résoudre des problèmes concernant les objets de cette… …   Wikipédia en Français

Share the article and excerpts

Direct link
… Do a right-click on the link above
and select “Copy Link”